箱ひげ図の作り方

≪箱ひげ図の作り方≫

◇この教材は，高校生が表計算ソフトを使って，数学Ⅰの「データ分析」レベルの内容を扱うときの「演習の手引き」として書いたものです．（筆者自身用の備忘録でもある）
◇●1～●4のソフトについて操作方法を解説していますが，全部読む必要はありません．自分のパソコンで使えるソフトを選んで，読んでください．

1.　四分位数

(1)　資料を小さい順に並べて，四分の一ずつにある点(25%点，50%点，75%点)を順に第1四分位数，第2四分位数，第3四分位数といい，それぞれQ1，Q2，Q3で表す．ただし，第2四分位数は中央値である．
(2)　最小値，第1四分位数，第2四分位数（中央値），第3四分位数，最大値の５つの数をまとめて，「５数要約」といい，これによりデータの散らばりが大まかに分かる．

2.　四分位数の決め方

　統計の教科書では，四分位数には幾つかの決め方があるとされているが，中学校・高等学校の教科書では，次の方法で四分位数を決める．これは，四分位数を「排他的な中央値」と呼ばれる方法で求める方法に，概ね対応している．（コンピュータの計算と，中高の教科書の説明は，データ総数が偶数のとき少しずれるが，詳細は後で述べる）

(1)　資料の総数が奇数個で，その中央値を取り除いた残りもそれぞれ奇数個であるとき

【例】合計11個の資料の場合
①②③④⑤⑥⑦⑧⑨⑩⑪
⇒⑥が中央値
　これを取り除いて，「小さい方の半分」「大きい方の半分」に分けて，それぞれ中央値を決める
①②③④⑤の中央値は③，⑦⑧⑨⑩⑪の中央値は⑨
⇒最小値=①，第1四分位数=③，第2四分位数=⑥，
　第3四分位数=⑨，最大値=⑪

※　四分位数は，平均値などと違って，各値がどれだけ離れているかなどとは関係なく「順序だけ」で決まることに注意
　例えば　①②⑤⑥⑦⑨⑩⑪⑬⑯⑱　の場合
⇒最小値=①，中央値=⑨，第1四分位数=⑤，第3四分位数=⑬，最大値=⑱ となる

(2)　資料の総数が奇数個で，その中央値を取り除いた残りがそれぞれ偶数個であるとき

【例】合計9個の資料の場合
①②|③④⑤⑥⑦|⑧⑨
⇒⑤が中央値
　これを取り除いて，「小さい方の半分」「大きい方の半分」に分けて，それぞれ中央値を決める
①②③④の中央値は②③の平均，⑥⑦⑧⑨の中央値は⑦⑧の平均
⇒最小値=①，第1四分位数=(②+③)÷2=2.5，第2四分位数=⑤，第3四分位数=(⑦+⑧)÷2=7.5，最大値=⑨

他の例では，　②④|④⑤⑧⑧⑮|⑰⑳　の場合
⇒⑧が中央値
　これを取り除いて，「小さい方の半分」「大きい方の半分」に分けて，それぞれ中央値を決める
②④④⑤の中央値は④④の中央値=④，（大きい方の⑧は取り除かないので）大きい方⑧⑮⑰⑳の中央値は⑮⑰の平均=⑯
⇒最小値=②，第1四分位数=④，第2四分位数=⑧，第3四分位数=⑯，最大値=⑳

(3)　資料の総数が偶数個で，中央値で２つに分けた組がそれぞれ奇数個であるとき

【例】合計10個の資料の場合
①②③④⑤|⑥⑦⑧⑨⑩
⇒(⑤+⑥)÷2=5.5が中央値
　「小さい方の半分」「大きい方の半分」に分けて，それぞれ中央値を決める
①②③④⑤の中央値は③，⑥⑦⑧⑨⑩の中央値は⑧
⇒最小値=①，第1四分位数=③，第2四分位数=5.5，第3四分位数=⑧，最大値=⑩

(4)　資料の総数が偶数個で，中央値で２つに分けた組もそれぞれ偶数個であるとき

【例】合計8個の資料の場合
①②|③④|⑤⑥|⑦⑧
⇒(④+⑤)÷2が中央値
　「小さい方の半分」「大きい方の半分」に分けて，それぞれ中央値を決める
①②③④の中央値は(②+③)÷2，⑤⑥⑦⑧の中央値(⑥+⑦)÷2
⇒最小値=①，第1四分位数(②+③)÷2，第2四分位数=(④+⑤)÷2，第3四分位数(⑥+⑦)÷2，最大値=⑧

3.　パソコンを使った四分位数の計算

　ここでは，次の４つの方法について，実際に行った結果をまとめたものです．
　全部読む必要はありません．自分のパソコンで使える箇所を選んで，読んでください．

●1「Microsoft Excel 2021」（インストール型）
●2　無料で使える「Excel for the web」
●3　無料で使える「Google スプレッドシート」
●4　無料でインストールできる統計用ソフト「R」

　Excelで四分位数を求める関数は，ア）Quartile(), イ）Quartile.exc(), ウ）Quartile.inc()の3つある．アは，旧バージョンのExcelで作られたワークシートでも使えるように（下位互換性を維持するために）残されているもの．イは中学校・高等学校の教科書での四分位数計算の決め方，すなわちExcelでの「排他的な中央値」に対応している（excはexclusive：排他的なの略．）ウは，後に述べる箱ひげ図を考案したアメリカの統計学者テューキーが考えた決め方，すなわちExcelでの「包括的な中央値」に対応している（incはinclusive：包括的なの略．）
　中学・高校の授業で，四分位数を計算するとき，●1，●2，●3では，イ）のQuartile.exc()を使う．●4では，パラメータをtype=6, 2,5などの形で指定するとできるようです．
（以下の記述は，ソフトのマニュアル･HELPに書かれていなくて，2023年現在でweb記事でもちょうど合う解説が見つからなかったものについて，筆者が数十回テストした結果をまとめたものです．･･･つまり，文献の裏付けはありません．個人の感想ですが，これがないと実際に困るので，まとめたものです）

	●1	●2	●3	●4
(1)(2)総数が奇数の場合	◎			◎
(3)(4)総数が偶数の場合	〇▼			◎

◎印:できる,〇:概ねできる,▼:薦めない

!!このまとめは，このページの最後の方（箱ひげ図の作り方）まで引きずっていきます!!

(1)(2)総数が奇数の場合

●1，●2，●3とも ⇒ ◎:できる

=QUARTILE.EXC(データの範囲, 戻り値)

の形で使う．戻り値1の場合は，第1四分位数:Q1，戻り値2の場合は，第2四分位数（中央値）:Q2，戻り値3の場合は，第3四分位数:Q3が返される．

2.(1)で示した例
「総数が奇数個で，中央値を取り除いた上組も下組も奇数になる場合」

1,2,5,6,7,9,10,11,13,16,18

の11個のデータについて，（セルの範囲 A1～A11 にあるとする）

=QUARTILE.EXC(A1:A11, 1)

⇒ 5 （第1四分位数:Q1）

=QUARTILE.EXC(A1:A11, 2)

⇒ 9 （第2四分位数:Q2）

=QUARTILE.EXC(A1:A11, 3)

⇒ 13（第3四分位数:Q3）

が得られる．

♪♥♫（まじめな雑談）♣♬∅♠
　●1. Excel2021, ●2. Excel on the web, ●3. Googleスプレッドシートで四分位数を求める関数は
　　quartile（日本語：四分位）
であるが，●4. 「R」で四分位数を求める関数は
　　quantile（日本語：四分位数）
　自慢じゃないが，老眼・近眼・乱視の筆者には，同じに見えるので適当に入力していると，エラーになる･･･ビックリ！

●4 ⇒ ◎:できる

• 四分位数を返す関数 Quantile()を使う場合

d1<-c(1,2,5,6,7,9,10,11,13,16,18)
quantile(d1,type=6)

　type=6 が排他的な中央値を返す

⇒ 0% 25% 50% 75% 100%
　1 　5 　9 　13 　18

• 5数要約を返す関数 Summary()を使う場合

d1<-c(1,2,5,6,7,9,10,11,13,16,18)
summary(d1, quantile.type=6)

　quantile.type=6 が排他的な中央値を返す

⇒ Min. 1st Qu. Median Mean 3rd Qu. Max.
　 1.000 　5.000 　9.000 　8.909 　13.000 　18.000

（平均値 Meanも出力される）

2.(2)で示した例:
「総数が奇数個で，中央値を取り除いた上組も下組が偶数になる場合」

2,4,4,5,8,8,15,17,20

の9個のデータについて，（セルの範囲 B1～B9 にあるとする），
●1，●2，●3とも ⇒ ◎:できる

=QUARTILE.EXC(B1:B9, 1)

⇒ 4 （第1四分位数:Q1）

=QUARTILE.EXC(B1:B9, 2)

⇒ 8 （第2四分位数:Q2）

=QUARTILE.EXC(B1:B9, 3)

⇒ 16（第3四分位数:Q3）

が得られる．

●4 ⇒ ◎:できる

• 四分位数を返す関数 Quantile()を使う場合

d2<-c(2,4,4,5,8,8,15,17,20)
quantile(d2,type=6)

　type=6 が排他的な中央値を返す

⇒ 0% 25% 50% 75% 100%
　2 　4 　8 　16 　20

• 5数要約を返す関数 Summary()を使う場合

d2<-c(1,2,5,6,7,9,10,11,13,16,18)
summary(d2, quantile.type=6)

　quantile.type=6 が排他的な中央値を返す

⇒ Min. 1st Qu. Median Mean 3rd Qu. Max.
　2.000 　4.000 　8.000 　9.222 　16.000 　20.000

（平均値 Meanも出力される）

(3)(4)総数が偶数の場合

●1，●2，●3とも ⇒ 〇:概ねできるが，▼：少数では無理･･･

ア
2.(3)で示した例
「総数が偶数個で，中央値の上組も下組も奇数になる場合」

1,2,3,4,5, 6,7,8,9,10

の10個のデータについて

⇒ 中学・高校の授業では，Q2=5.5, Q1=3, Q3=8

（セルの範囲 A1～A10 にあるとする），●1，●2，●3とも

=QUARTILE.EXC(A1:A10, 1)

⇒ 2.75 （第1四分位数:Q1）

=QUARTILE.EXC(A1:A10, 2)

⇒ 5.5 （第2四分位数:Q2）

=QUARTILE.EXC(A1:A10, 3)

⇒ 8.25（第3四分位数:Q3）

　web記事などで，簡単な説明が見つからないので推定する．読者が覚えやすいように，なるべく情緒的な用語を使って，動揺しやすい審判をイメージしながら説明する．
　中央値5.5はよい．
　全体が偶数だったときは，上下の組も偶数になるように，5も6も「中央値の代わりに削除して」1,2,3,4から下組の中央値を求めるが，5を厳しく削除した埋め合わせとして，2,3の中央値でなく，（中央寄りに）3:1に内分した点2.75とする．
　上組も同様に，初め厳しく6も削除する代わりに，その埋め合わせとして，8,9の中央値でなく，1:3に（中央寄りに）内分した点8.25とする．

イ
他の例

1,2,6,6,10, 12,13,15,19,20

⇒ 中学・高校の授業では，Q2=11, Q1=6, Q3=15

●1，●2，●3とも，
中央値は11として，

⇒ 11 （第2四分位数:Q2）

全体が偶数だったときは，上下の組も偶数になるように，10と12も削除して，その埋め合わせとして，2,6を（中央寄りに）3:1に内分する点を求めて5とする．

⇒ 5 （第2四分位数:Q1）

同様にして，15,19を（中央寄りに）1:3に内分する点を求めて16とする．

⇒ 16 （第2四分位数:Q3）

ウ
2.(4)で示した例
「総数が偶数個で，中央値の上組も下組も偶数になる場合」

1,2,3,4, 5,6,7,8

の8個のデータについて

⇒ 中学・高校の授業では，Q2=4.5, Q1=2.5, Q3=6.5

●1，●2，●3とも（セルの範囲 A1～A8 にあるとする）

=QUARTILE.EXC(A1:A8, 1)

⇒ 2.25 （第1四分位数:Q1）

=QUARTILE.EXC(A1:A8, 2)

⇒ 4.5 （第2四分位数:Q2）

=QUARTILE.EXC(A1:A8, 3)

⇒ 6.75（第3四分位数:Q3）

中央値は4.5
全体が偶数だったときは，上下の組も偶数になるように，4と5も削除せず，その埋め合わせとして，2,3を（端寄りに）1:3に内分する点を求めて2.25とする
同様にして，6,7を（端寄りに）3:1に内分する点を求めて6.75とする．

エ
他の例

1,2,7,9,13,14,17,20,
22,25,27,30,34,38,40,41

の16個のデータでは，
●1，●2，●3とも，
　中央値は21
　20と22も削除せず，その埋め合わせとして，9,13を（端寄りに）1:3に内分する点を求めて10とする
　同様に，30,34を（端寄りに）3:1に内分する点を求めて33とする

⇒ 以上のア～エのいずれも，●1，●2，●3の方法で，第1四分位数:Q1，第3四分位数:Q3が，中学・高校の教え方とちょうど合うものはない．
⇒ 目で見て，計算するしかない
　四分位数を用いた散らばり具合の分析は，総数が数十とか数百という普通に出あう大きなデータに対しては，些細な相違はほとんど影響しないが，データ数が10個程度の場合，中学・高校の教科書で教える四分位数計算の決め方とExcelなどコンピュータソフトで計算した結果とは，食い違うことがある．
　この結果は，箱ひげ図にも反映する．

　ア～エの特徴がExcelのHELPに書かれている訳ではない．筆者が数十回も実験したらこうなったという結果をまとめたものです

●4 ⇒ ◎：できるが，△：コテコテする･･･
2.(4)で示した例

1,2,3,4,5,6,7,8,9,10

の10個のデータについて， • 四分位数を返す関数 Quantile()を使う場合

d3<-c(1,2,3,4,5,6,7,8,9,10)
quantile(d3,type=2)

　type=2 または type=5 がデータ数が偶数のときに，中高の教え方と一致する排他的な中央値を返す

⇒ 0% 25% 50% 75% 100%
　1.0 　3.0 　5.5 　8.0 　10.0

• 5数要約を返す関数 summary()を使う場合

d3<-c(1,2,3,4,5,6,7,8,9,10)
summary(d3, quantile.type=2)

または

d3<-c(1,2,3,4,5,6,7,8,9,10)
summary(d3, quantile.type=5)

　quantile.type=2または quantile.type=5 が中高の教え方と一致する排他的な中央値を返す

⇒ Min. 1st Qu. Median Mean 3rd Qu. Max.
　　1.0 　3.0 　5.5 　5.5 　8.0 　10.0

（平均値 Meanも出力される）

他の例
1,2,7,9,13,14,17,20,22,25,27,30,34,38,40,41
の16個のデータでは，

d4<-c(1,2,7,9,13,14,17,20,22,25,27,30,34,38,40,41)
quantile(d4,type=2)

または

d4<-c(1,2,7,9,13,14,17,20,22,25,27,30,34,38,40,41)
quantile(d4,type=5)

により

⇒ 0% 25% 50% 75% 100%
　　1 　11 　21 　32 　41

同様に

d4<-c(1,2,7,9,13,14,17,20,22,25,27,30,34,38,40,41)
summary(d4, quantile.type=2)

または

d4<-c(1,2,7,9,13,14,17,20,22,25,27,30,34,38,40,41)
summary(d4, quantile.type=5)

により

⇒ Min. 1st Qu. Median Mean 3rd Qu. Max.
　1.00 　11.00 　21.00 　21.25 　32.00 　41.00

■ここまでの実験結果の要約■
ア）データ総数=奇数個，上組下組とも奇数個となる例

数値の組	中高の教え方	●1,2,3 =QUARTILE.EXC(*1)	●4 quantile(2) summary(3)
1,2,3,4,5,6,7 (7個→3個,3個)	Q1=2 Q2=4 Q3=6	2 4 6	2 4 6
2,3,4,5,6,7,8, 9,10,11,12 (11個→5個,5個)	Q1=4 Q2=7 Q3=10	4 7 10	4 7 10
3,4,5,6,7,8,9,10,11, 12,13,14,15,16,17 (15個→7個,7個)	Q1=6 Q2=10 Q3=14	6 10 14	6 10 14

*1は，Q1のとき，(データ範囲,1)，Q2のとき，(データ範囲,2)，Q3のとき，(データ範囲,3)とする
*2は，(データ,type=6)とする
*3は, (データ,quantile.type=6)とする

イ）データ総数=奇数個，上組下組とも偶数個となる例

数値の組	中高の教え方	●1,2,3 =QUARTILE.EXC(*1)	●4 quantile(2) summary(3)
1,2,3,4,5,6,7,9,10 (9個→4個,4個)	Q1=2.5 Q2=5 Q3=8	2.5 5 8	2.5 5 8
1,2,3,4,5,6,7,9, 10,12,13,14,15 (13個→6個,6個)	Q1=3.5 Q2=7 Q3=12.5	3.5 7 12.5	3.5 7 12.5
1,2,3,4,5,6,7,8,9, 10,11,12,13,14, 15,16,17 (17個→8個,8個)	Q1=4.5 Q2=9 Q3=13.5	4.5 9 13.5	4.5 9 13.5

*1, *2, *3はアと同様

ウ）データ総数=偶数個，上組下組とも奇数個となる例

数値の組	中高の教え方	●1,2,3 =QUARTILE.EXC(*1)	●4 quantile(2) summary(3)
1,3,5,7,9,11,13, 15,17,19,21,23, 25,27 (14個→7個,7個)	Q1=7 Q2=14 Q3=21	6.5 14 21.5	7 14 21
1,3,5,7,9,11,13, 15,17,19,21,23,25, 27,31,33,35,37 (18個→9個,9個)	Q1=9 Q2=18 Q3=27	8.5 18 28	9 18 27
1,3,5,7,9,11,13, 15,17,19,21,23,25, 27,31,35,37,39,41, 43,45,47 (22個→11個,11個)	Q1=11 Q2=22 Q3=37	10.5 22 37.5	11 22 37

*1は，Q1のとき，(データ範囲,1)，Q2のとき，(データ範囲,2)，Q3のとき，(データ範囲,3)とする
*2は，(データ,type=2)または(データ,type=5)とする
*3は, (データ,quantile.type=2)または(データ,quantile.type=5)とする

エ）データ総数=偶数個，上組下組とも偶数個となる例

数値の組	中高の教え方	●1,2,3 =QUARTILE.EXC(*1)	●4 quantile(2) summary(3)
1,2,3,6,7,8, 9,10,11,12,14,16 (12個→6個,6個)	Q1=4.5 Q2=8.5 Q3=11.5	3.75 8.5 11.75	4.5 8.5 11.5
1,2,3,4,5,6, 7,8, 9,10,11,12, 12,14,15,16 (16個→8個,8個)	Q1=4.5 Q2=8.5 Q3=12	4.25 8.5 12.75	4.5 8.5 12
1,2,6,7,8,10,10, 11,12,13,14,15,16,17, 18,19,21,21,22,23 (20個→10個,10個)	Q1=9 Q2=13.5 Q3=18.5	8.5 13.5 18.75	9 13.5 18.5

*1, *2, *3はウと同様

⇒ 以上のように，●4の方法では，
• データ総数が奇数のときは

quantile(データ,type=6) または summary(データ, quantile.type=6)

により，中学・高校の教え方と一致する結果が得られる．
• データ総数が偶数のときは

quantile(データ,type=○) ○=2,5 または summary(データ, quantile.type=○) ○=2, 5

により，中学・高校の教え方と一致する結果が得られる．

　Rのマニュアルにこのように書かれている訳ではない．筆者が数十回も実験したらこうなったという結果をまとめたものです

4.　ここまでの復習

　次のデータが与えられているとき，目の子算で（目で見た暗算で），中学・高校の教え方と一致する四分位数を求めてください．また，パソコンを使って，その結果を確かめてください．

【問題1】
　2,4,5,6,7,10,12,13,15,18,20

【解答】
Q1=5, Q2=10, Q3=15･･･（答）
　（データ総数が11個:奇数だから）パソコンでは，●1，●2，●3のいずれも，=QUARTILE.EXC(データ範囲, 1), =QUARTILE.EXC(データ範囲, 2), =QUARTILE.EXC(データ範囲, 3) で結果が得られる．
　●4では，

d1<-c(2,4,5,6,7,10,12,13,15,18,20)
quantile(d1,type=6)
または
summary(d1,quantile.type=6)

により，上記の結果が得られる．

【問題2】
　3,6,9,10,12,15,16,18,20,22,25,26,28

【解答】
Q1=9.5, Q2=16, Q3=23.5･･･（答）
　（データ総数が13個:奇数だから）パソコンでは，●1，●2，●3のいずれも，=QUARTILE.EXC(データ範囲, 1), =QUARTILE.EXC(データ範囲, 2), =QUARTILE.EXC(データ範囲, 3) で結果が得られる．
　●4では，

d2<-c(3,6,9,10,12,15,16,18,20,22,25,26,28)
quantile(d2,type=6)
または
summary(d2,quantile.type=6)

により，上記の結果が得られる．

【問題3】
　1,3,5,7,9,11,13,15,17,19,21,23,25,28

【解答】
Q1=7, Q2=14, Q3=21･･･（答）
（データ総数が14個:偶数だから）パソコンでは，●1，●2，●3のいずれも，中央値 =QUARTILE.EXC(データ範囲, 2)の結果のみ一致する．他は合わない．
　●4では，

d3<-c(1,3,5,7,9,11,13,15,17,19,21,23,25,28)
quantile(d3,type=2)もしくはquantile(d3,type=5)
または
summary(d3,quantile.type=2)もしくはsummary(d3,quantile.type=5)

により，上記の結果が得られる．

【問題4】
　2,5,8,11,14,17,20,23,26,29,32,35

【解答】
Q1=9.5, Q2=18.5, Q3=27.5･･･（答）
（データ総数が14個:偶数だから）パソコンでは，●1，●2，●3のいずれも，中央値 =QUARTILE.EXC(データ範囲, 2)の結果のみ一致する．他は合わない．
　●4では，

d4<-c(2,5,8,11,14,17,20,23,26,29,32,35)
quantile(d4,type=2)もしくはquantile(d4,type=5)
または
summary(d4,quantile.type=2)もしくはsummary(d4,quantile.type=5)

により，上記の結果が得られる．

5.　箱ひげ図

==中学校の復習==

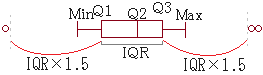
• 最小値，第1四分位数，第2四分位数（中央値），第3四分位数，最大値を次のように視覚的に表したものを「箱ひげ図」という．

• 最大値と最小値の差を「範囲」という．
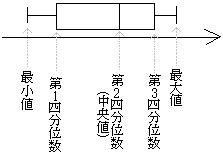• 第3四分位数と第1四分位数の差を「四分位範囲」という．
• 範囲や四分位範囲によって，資料の散らばり具合が分かる.

♥==高校入試問題（復習）==♠

-- 手書きで「箱ひげ図」を描く場合

♪基本の確認は♬ ⇒ 【こちら】

《データ総数が奇数個，上下2組とも奇数個》の問題例

表(単位:点)
13, 7, 19, 10, 5, 11, 14, 20, 7, 8, 16

【問題1】
　右の表は，クイズ大会に参加した11人の得点である。この表をもとにして，箱ひげ図をかくと，右の図のようになった。a, bの値をそれぞれ求めなさい。

（2022年度徳島県公立高校入試問題）

（解答）
• 資料を小さい順に並べると
　　5,7,[7],8,10, (11),13,14,[16],19, 20 となる．
• 11個の資料で小さい順に6番目の 11 が中央値（第2四分位数）
• それを取り除いた残り２組について，下の組の中央値 7が第1四分位数，上の組の中央値16が第3四分位数
したがって，a=7, b=16…（答）

【問題2】
　次の【データ】は，ある生徒15人について，小テストを実施したときの全員の得点を，値の小さい順に並べたものである。
【データ】

4, 6, 6, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24,
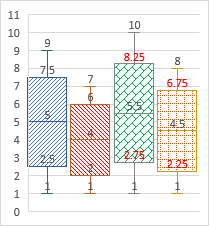
28, 30　(単位：点)

(点) 30 26 22 18 14 10 6 2 ① ② ③ ④

　この【データ】を表した箱ひげ図として正しいものを，右の①～④の中から１つ選び，番号を書きなさい。

（2022年度佐賀県公立高校入試問題）

（解答）
4,6,6,[6],8,10,12,(14),16,18,20,[22],24,28,30
⇒ 最小値=4,第1四分位数=6, 第2四分位数=14, 第3四分位数=22, 最大値=30だから②…（答）

==パソコンを使う場合の「箱ひげ図の作成」==

表1
得点
38
40
44
46
54
63
78
82
82
85
92

5数要約

Max	98
Q3	82
Q2	63
Q1	44
min	38

箱ひげ図

Ⅰ　表1のように与えられたデータから，（直接）箱ひげ図を作れるか
Ⅱ　表1のように与えられたデータから，５数要約の計算をして，箱ひげ図を作れるか

【要約】　《筆者の実験結果です．異論はあり得ます》
●1「Microsoft Excel 2021」（インストール型）
●2　無料で使える「Excel for the web」
●3　無料で使える「Google スプレッドシート」
●4　無料でインストールできる統計用ソフト「R」

	●1	●2	●3	●4
Ⅰ データから直接箱ひげ図	〇	〇	▼	〇
Ⅱ ５数要約表経由で箱ひげ図	▼	▼	▼	◎

◎印:できる,〇:概ねできる,▼:薦めない

Ⅰ
　●1,2は，「データから直接に箱ひげ図」ができ，さらに「箱ひげ図に値のラベルも付けられる」が，データ総数が偶数のとき，Q1，Q3の値が，中学・高校の教え方と合わない．
　●4は，「データから直接に箱ひげ図」ができるが，「箱ひげ図に値のラベルは付けられない」．
Ⅱ
　●1,2で，５数要約表から箱ひげ図を作るのは，薦められない．

Ⅰ　表1のように与えられたデータから，（直接）箱ひげ図を作れるか

●1　「Microsoft Excel 2021」（インストール型）

〇:概ねできる

　データ総数が，数十，数百のときは細部を気にしなくてもよいでしょう．ただし，「データ総数が30以下のような小さい数字」かつ「データ総数が偶数」であるときは，得られたグラフのQ1，Q3の値が，中学・高校で習った内容と合わない場合がある．

(1)　表1のデータがExcel上にあるとして，列タイトル（得点）を含めて，データ範囲をドラッグして反転表示にする．
(2)　挿入→（グラフの一群のアイコンを探すが，ピッタリのものがないので $\searrow$ のマークをクリックして，「すべてのグラフ」というタブを選択する）→箱ひげ図
(3)　ここまでの作業で，箱ひげ図が表示される
(4)　グラフをポイントすると，画面右側に「グラフエリアの書式設定」ウィンドウが表示され，箱ひげ図の色，枠線，塗り方パターンが選べる
(5)　再び，グラフをポイントして，グラフの右上に表示されれている＋のアイコンをクリック．データラベルにチェックを入れて，右などを選ぶ
(6)　以下の部分は､慎重にしないとできない！
グラフ全体ではなく，箱ひげ図の部分だけをポイントして，「排他的な中央値」にラジオボタンがあることを確かめる．（確かめなくても，デフォルトでそれが選ばれるが，「排他的な中央値」を選んでいることを認識することが重要）

　ついでに「平均マーカーを表示する」にチェックが入っていることを確かめる．箱ひげ図の中に５数要約に含まれない「平均」も，×印によって，表示される（平均が不要な場合は，チェックを外す）．
　このグラフに表示された数字が（特に，Q1とQ3）「排他的な中央値」の計算方法によって求められた数字と一致していることが重要

　データの個数は11個で，中央値はQ2=63．次に，「排他的な中央値」として，63を取り除いて，下組「38,40,44,46,54」の中央はQ1=44，上組「78,82,82,85,92」の中央はQ3=82
　最小値は38，最大値は92．なお，平均は×印の64

●2　無料で使える「Excel for the web」

⇒導入方法は前のページ

〇:概ねできる

　「データ総数が30以下のような小さい数字」かつ「データ総数が偶数」であるとき，●1と同様の問題点がある．

　作業手順は，●1とほぼ同じ．
　(2)でグラフを探すのは∨のアイコンからグラフを全部表示して，箱ひげ図を選ぶ．
　書式設定で，データラベルで値にチェックを入れる．（塗りこみで斜線パターンは選べない）

●3　無料で使える「Google スプレッドシート」

⇒導入方法は前のページ
▼：お薦めしない
　Googleスプレッドシートでは，与えられたデータから直接に箱ひげ図を作成することは無理です．Ⅱの5数要約を経由しても，箱ひげ図そのものは選べない．
　第2四分位数（中央値）を除いた，最小値，Q1，Q3，最大値の4つの値からローソク図を作ることはできるが，ひげの部分がＴ字型に表示されない．

●4　無料でインストールできる統計用ソフト「R」

⇒導入方法は前のページ
◎:できる

• Rのコマンドプロンプトから，次のように入力する．

d1<-c(38,40,44,46,54,63,78,82,82,85,92)
boxplot(d1,type=6)

ここまでで，右図の散布図が描かれる．
同時に，次の5数要約がRのコンソール画面に表示される

• 「R」で「排他的な中央値」を指定するには，パラメータとして，type=6を書き込む
• Excelの場合と同様に，箱ひげ図に値を記入する方法は？

Ⅱ　表1のように与えられたデータから，５数要約の計算をして，箱ひげ図を作れるか

●1　「Microsoft Excel 2021」（インストール型）

▼：お薦めしない

表2
B	C
戻り値	四分位数
0	#NUM!
1	44
2	63
3	82
4	#NUM!

表1(再掲)
	A
1	得点
2	38
3	40
4	44
5	46
6	54
7	63
8	78
9	82
10	82
11	85
12	92

　右の表1のような元のデータから，=Quartile.exc()関数を利用して，表2のような５数要約を作ることはできる．
　ただし，=Quartile.exc()関数は，戻り値が0,4のときは，#NUM!（数字でない）を返す仕様になっているので，0の横には，最小値を求める関数 =min()を，4の横には，最大値を求める関数 =max()を書く．
　このようにすれば，中高の教科書通りの排他的中央値を用いた５数要約になるが，表2から箱ひげ図を作っても，求めたものは得られない．
　Excelでこの作業を行うと，表1に示された元のデータに対する箱ひげ図ではなく，新たに作られた表2の5つの数に対する箱ひげ図を作ってしまうので，ここで想定したものとは違うものになる．

●2　無料で使える「Excel for the web」

▼：お薦めしない
　●1と同様

●3　無料で使える「Google スプレッドシート」

⇒導入方法は前のページ
▼：お薦めしない
　Googleスプレッドシートでは，Ⅱの5数要約を経由しても，箱ひげ図そのものは選べない．
　第2四分位数（中央値）を除いた，最小値，Q1，Q3，最大値の4つの値からローソク図を作ることはできるが，ひげの部分がＴ字型に表示されない．

●4　無料でインストールできる統計用ソフト「R」

⇒導入方法は前のページ
◎:できるが，データから直接描いたものと同じになる

• Rのコマンドプロンプトから，次のように入力する．

d1<-c(38,40,44,46,54,63,78,82,82,85,92)
dd1<-quantile(d1,type=6)
boxplot(dd1)

または

d1<-c(38,40,44,46,54,63,78,82,82,85,92)
dd1<-summary(d1,quantile.type=6)
boxplot(dd1)

ここまでで，右図の散布図が描かれる．
同時に，次の5数要約がRのコンソール画面に表示される
Min. 1st Qu. Median Mean 3rd Qu. Max.
　38 　44 　63 　64 　82 　92

7.　複数系列の箱ひげ図の表示

　次の表3のデータから，右図1の形で，国語，数学，英語，理科の４つの系列の箱ひげ図を表示したいものとする．だたし，No.10の生徒の国語の得点など空欄は欠席で，そのセルには何も書かれていないとする．

-表3-
名前	国語	数学	英語	理科
No.1	1	1	1	1
No.2	2	2	2	2
No.3	3	3	3	3
No.4	4	4	4	4
No.5	5	5	5	5
No.6	6	6	6	6
No.7	7	7	7	7
No.8	8		8	8
No.9	9		9
No.10			10

-図1-

　Excel上での作業を分かりやすくするため，名前というセルはA1，No.11の生徒の理科の得点（空欄）は，E11だとする．

●1　「Microsoft Excel 2021」（インストール型）

〇:概ねできる

　図1のグラフまでできるが，英語と理科のデータが偶数個であるため，ここまでの解説で述べたように，赤字で示したQ1，Q3の値が，中高の授業で教える数字とわずかに違うので「〇:概ねできる」という評価になった．

(1)　表3のB1（国語）からE11まで，データ範囲をドラッグして反転表示にする．
(2)　挿入→（グラフの一群のアイコンを探すが，ピッタリのものがないので $\searrow$ のマークをクリックして，「すべてのグラフ」というタブを選択する）→箱ひげ図
(3)　ここまでの作業で，箱ひげ図が表示される
(4)　グラフをポイントすると，画面右側に「グラフエリアの書式設定」ウィンドウが表示され，箱ひげ図の色，枠線，塗り方パターンが選べる
(5)　再び，グラフをポイントして，グラフの右上に表示されれている＋のアイコンをクリック．データラベルにチェックを入れて，右などを選ぶ
(6)　グラフ全体ではなく，箱ひげ図の部分だけをポイントして，「排他的な中央値」にラジオボタンがあることを確かめる．（確かめなくても，デフォルトでそれが選ばれるが，「排他的な中央値」を選んでいることを認識することが重要）
　今回は，「平均マーカーを表示する」のチェックを外して（中央値と近過ぎて，値の表示が被るから）箱ひげ図の中に５数要約に含まれない「平均」は表示しないことにする．（一度に設定できないときは，１つずつ行う）

●2　無料で使える「Excel for the web」

〇:概ねできる

　●1とほぼ同様にできる

●3　無料で使える「Google スプレッドシート」

▼：お薦めしない
　Googleスプレッドシートでは，箱ひげ図は選べない．

●4　無料でインストールできる統計用ソフト「R」

◎:できる

• Rのコマンドプロンプトから，次のように入力する．

d1<-c(1,2,3,4,5,6,7,8,9)
d2<-c(1,2,3,4,5,6,7)
d3<-c(1,2,3,4,5,6,7,8,9,10)
d4<-c(1,2,3,4,5,6,7,8)
subject1<-c("国語","数学","英語","理科")
boxplot(d1,d2,d3,d4,names=subject1)

　これで，複数系列の箱ひげ図が表示されているが，よく見ると，Q1，Q3の値がデフォルトで「包括的な中央値」(inclusive)になっているので，奇数個のd1，d2はtype=6に，偶数個のd3,d4はtype=5に設定しなおすと次のようになる．

d1<-c(1,2,3,4,5,6,7,8,9)
d2<-c(1,2,3,4,5,6,7)
d3<-c(1,2,3,4,5,6,7,8,9,10)
d4<-c(1,2,3,4,5,6,7,8)
dd1<-quantile(d1,type=6)
dd2<-quantile(d2,type=6)
dd3<-quantile(d3,type=5)
dd4<-quantile(d4,type=5)
subject1<-c("国語","数学","英語","理科")
boxplot(dd1,dd2,dd3,dd4,names=subject1)

　これにより，中高の教え方と合う，次の値のグラフになる．

	Min	Q1	Q2	Q3	Max
国語	1	2.5	5	7.5	9
数学	1	2	4	6	7
英語	1	3	5.5	8	10
理科	1	2.5	4.5	6.5	8

　●4のRでは横向き箱ひげ図の表示：パラメータとして，horizontal=T または horizontal=TRUE を追加すると，次の図のように横向きの箱ひげ図になる．
　●1,●2のExcelでは，横向きの箱ひげ図は用意されていない．

7.　外れ値の表示

　データの中で，他の値から極端にかけ離れた値を外れ値はずれちという．
　例えば，平均年収が500万円の住人9世帯が住んでいる町内に，年収1億円のお金持ちが引っ越して来たら，その町内の平均年収は1450万円となって，町内の住人の年収からはかけ離れた値になる．このように，「平均」は外れ値に影響されやすいが，中央値は影響を受けない．
　ここでは，外れ値が含まれる場合の箱ひげ図の描き方を扱う．

(1)　四分位範囲（IQR）の定義
　第3四分位数Q3と第1四分位数Q1の差を四分位範囲といい，IQRで表す．

IQR=Q3−Q1

　「第1四分位数よりもIQRの1.5倍以上小さい値」「第3四分位数よりもIQRの1.5倍以上大きい値」を外れ値という．

x≦Q1−IQR×1.5
x≧Q3+IQR×1.5

　箱ひげ図において

（※）「外れ値を表示する」場合は，外れ値を○印（×印，＊印）で示し，それを取り除いたデータで最大値や最小値でひげの部分を描く．
［教科書］S社：○印，K社：＊印，D社：×印
［ソフト］●1●2：○印，●4：デフォルトで○印

なお，外れ値が（大きい側だけでも）2個以上の場合もあり得る．

(2)　外れ値の図示
　次の表3のデータにおいて，A群，B群ともQ1=5，Q2=9, Q3=13だから，四分位範囲IQR=13−5=8 である．したがって，外れ値は

x≦Q1−IQR×1.5=−7･･･該当なし
x≧Q3+IQR×1.5=25･･･26が該当する

　そこで，A群では外れ値はないが，B群の26は外れ値に該当する．

表3
A群	B群
1	1
2	2
5	5
6	6
7	7
9	9
10	10
11	11
13	13
16	16
25	26

　上記の(1) （※）「外れ値を表示する」場合は，･･･の記述を素朴に読めば，「外れ値を表示しない」場合は，例えば表3のB群の場合，ひげを26の値まで伸ばした図を描くように読める．（手書きではそうすればよい）
　しかし，●1,2で「特異ポイントを表示する」にチェックを入れない，もしくは●4のソフトでパラメータとして「 boxplot(データ, outline=F) 」を選ぶと，上記のB群の図で外れ値のマーク（○26）を単に書かないだけの図（最大値16をひげの上端とする図）が描かれるので注意．●1,2,●4とも「外れ値を表示する」を選ばなければ，外れ値はそもそも表示されない．

【問題4】
　次のデータについて，外れ値の有無を調べて，箱ひげ図を図示してください．
4,6,7,10,11,12,12,14,23

【解答】
Q1=6.5, Q2=11, Q3=13
四分位範囲 IQR=13−6.5=6.5

x≦Q1−IQR×1.5=−3.25･･･該当なし
x≧Q3+IQR×1.5=22.75･･･23が該当する

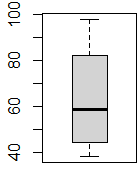
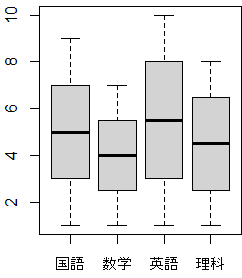
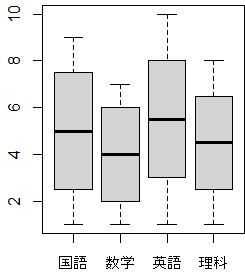
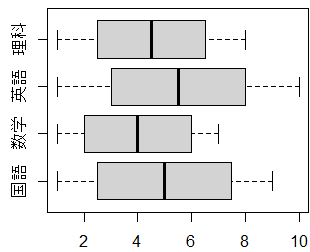
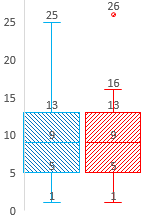
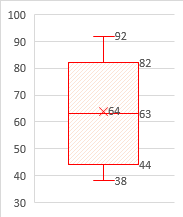
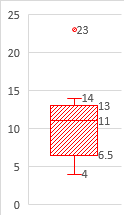●1，●2は右図のようになる
●4では，

d5<-c(4,6,7,10,11,12,12,14,23)
boxplot(d5)

により，同様の図が得られる．（数値ラベルは付かない）

...メニューに戻る

■このサイト内のGoogle検索■