背理法

← PC用は別頁

== 背理法の入試問題 ==

イラストによる背理法の説明(1)

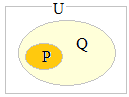
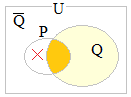
　qとqで世界の全部です．これ以外にはありません

条件qとqに対応する集合をQとQで表すとき，Q∪Q=U(全体集合)になります．

　このとき，p⇒qを証明したいが，pからqを直接証明するのが困難な場合，
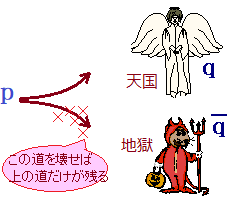
行きたくない方の道qに進んでみて，そちらに進めば世界が破滅してしまう（矛盾がある）ことを言う．この論法が背理法です．

（おとぎばなしによる解説）
地獄に行って，地獄を壊してしまうと天国だけが残ります・・・地獄に行かないと天国には行けません．

＃～地獄を見たものにしか，天国なんて分かるはずはないのだ，クソ－負けてたまるか～＃
と自分に言い聞かせると覚えやすい

（実際の手順）
pとqを仮定して矛盾を示す．（pも仮定することを忘れないように）

p
かつ
q⇒p

という形でpとpが矛盾するという構造でもよい．

→(数学的常識に反すること：1+1=1など)

p
かつ
q

という構造でもよい．

イラストによる背理法の説明(2)

P⊂Qとは
P：卵の黄身が
Q：卵の白身の
中にあることだと思えばよい

　論理的な関係p⇒q（pならばq）は，集合ではP⊂Qに対応します．
　言い換えれば，集合の関係としてP⊂Qとなっていることを示せば，p⇒qの証明になります．
　この証明は，集合P, Qの関係が一般のゆるい関係，すなわちP独自の部分，Q独自の部分，P, Qの共通部分から成り立っているのではなく，

P∩Qが空集合になることを言えばよい．（右図の×印の部分が空集合になることを言う）．
　そうすると「P：卵の黄身」は「Q：卵の白身」の中にある部分だけから成り立っていることになり，P⊂Qが言える．
　P∩Qが空集合になること（右図の×の部分には何もないこと）を示すには

「Pであって」かつ「Qである」ものが存在すると仮定すると，矛盾を生じることを示せばよい．

すなわち

　何かある要素xが，x∈Pかつx∈Qを満たすとすると具合の悪いことが起こることを示せばよい．

【要約】＜背理法とは＞
pとqを仮定して矛盾を示し，これによりp⇒qを証明する方法

※pも仮定することが重要．この点が対偶証明法と異なり，結論としてpが導ける場合に限られず，他の内容でも数学的に矛盾することが示せたら何でもよいので，自由度が大きい．

【例題１】
　 $\sqrt{2}$ は無理数であることを示せ．

（解答）
$\sqrt{2}$ が有理数であると仮定して矛盾を示す．
$\sqrt{2}=\frac{n}{m}$ （m, nは整数で互いに素）…(1)
と仮定すると
$2=\frac{n^2}{m^2}$
$2m^2=n^2$ …(2)
(2)において，左辺は2の倍数

もしも，nが奇数なら，n2は奇数となって，等式が成り立たないから，nは偶数でなければならない

n=2k（kは整数）…(3)
とおくと，(2)より
2m2=4k2
m2=2k2…(4)
(4)において，右辺は2の倍数

もしも，mが奇数なら，m2は奇数となって，等式が成り立たないから，mは偶数でなければならない

m=2l（lは整数）…(5)
とおくと，(3)と(5)はm, nは整数で互いに素という仮定に反するから矛盾．
よって， $\sqrt{2}$ が有理数であるという仮定は間違いであることが示されたから， $\sqrt{2}$ は無理数…(証明終)

　この証明の流れは，以下の問題において基本となるものなので，記憶に留めておくとよい．
　特に，(1)において一見些末(さまつ)なトリビアな話に聞こえる「互いに素」という「勝手な，ついでの話のような仮定」が設定してあって，それと矛盾することが証明の鍵となっているのだから，高校生が読んだら初めは違和感を持つかもしれません．
　ただし，整数÷整数の分数で書けるものは，約分できるだけ約分して既約分数にしておけるはずだから，無理な仮定ではない．
※初めはしっくりしないかもしれませんが，「次に出てきたら，真似してやろう」と息を潜めて構えているとよい．

【問題1.1】
　 $\sqrt[3]{2}$ は無理数であることを証明せよ． (2012年京都大学入試問題)

参考答案を見る参考答案を隠す

（解答）
$\sqrt[3]{2}$ が有理数であると仮定して矛盾を示す．
$\sqrt[3]{2}=\frac{n}{m}$ （m, nは整数で互いに素）…(1)
と仮定すると
$2=\frac{n^3}{m^3}$
2m3=n3…(2)
(2)において，左辺は2の倍数

もしも，nが奇数なら，n3は奇数となって，等式が成り立たないから，nは偶数でなければならない

n=2k（kは整数）…(3)
とおくと，(2)より
2m3=8k3
m3=4k3…(4)
(4)において，右辺は2の倍数

もしも，mが奇数なら，m2は奇数となって，等式が成り立たないから，mは偶数でなければならない

m=2l（lは整数）…(5)
とおくと，(3)と(5)はm, nは整数で互いに素という仮定に反するから矛盾．
よって， $\sqrt[3]{2}$ が有理数であるという仮定は間違いであることが示されたから， $\sqrt[3]{2}$ は無理数…(証明終) →閉じる←

【問題1.2】
素数pに対して， $\sqrt{p}$ は無理数であることを示せ．（富山大医学部2016年入試問題）

参考答案を見る参考答案を隠す

（解答）
$\sqrt{p}$ が有理数であると仮定して矛盾を示す．
$\sqrt{p}=\frac{n}{m}$ （m, nは整数で互いに素）…(1)
と仮定すると
$p=\frac{n^2}{m^2}$
$pm^2=n^2$ …(2)
(2)において，左辺はpの倍数

もしも，nがpの倍数でなければ，n2はpの倍数でなく，等式が成り立たないから，nはpの倍数でなければならない…(*)

n=pk（kは整数）…(3)
とおくと，(2)より
pm2=p2k2
m2=pk2…(4)
(4)において，右辺はpの倍数

もしも，mがpの倍数でなければ，m2はpの倍数でなく，等式が成り立たないから，mはpの倍数でなければならない…(**)

m=pl（lは整数）…(5)
とおくと，(3)と(5)はm, nは整数で互いに素という仮定に反するから矛盾．
よって， $\sqrt{p}$ が有理数であるという仮定は間違いであることが示されたから， $\sqrt{p}$ は無理数…(証明終)

※上記の答案で(*)(**)の部分は，書いてある内容に間違いはないが，証明としてやや甘いと判断される場合がある．もう少し詳しく書くと次のようになる．

もしも，nがpの倍数でなければ，
n=pk+r (0<r<p)
とおける．
このとき
n2=(pk+r)2=p2k2+2pkr+r2
=Np+r2 (Nは整数)
がpの倍数であれば，r2がpの倍数であることになる．
ところが，pは素数であるから，pよりも小さな整数r (0<r<p)の積 r2はpの倍数にはならない．

以上により，(*)が成り立つ．(**)も同様 →閉じる←

【問題1.3】
pが素数であるとき
$\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{p}$
は整数でないことを示せ．

参考答案を見る参考答案を隠す

（解答）

　 $\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{p}=n$ （nは整数）と仮定する
両辺に(p−1)!=1·2·3 ··· (p−1)を掛けると
$\frac{1}{1}\cdot (p-1)!,\hspace{5}\frac{1}{2}\cdot (p-1)!,\hspace{5}\frac{1}{3}\cdot (p-1)!,\hspace{5}...\frac{1}{p-1}\cdot (p-1)!$
と右辺のn·(p−1)!は整数になるが，左辺の $\frac{1}{p}\cdot (p-1)!$ は整数にならない．
　結局，左辺は整数でなく，右辺は整数になるから，矛盾

　したがって， $\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{p}=n$ が整数という仮定が間違っており，整数ではない →閉じる←

【問題1.4】
pが素数であるとき
$\log_{10}p$
は無理数であることを示せ．

参考答案を見る参考答案を隠す

（解答）
$\log_{10}p$ が有理数であると仮定して矛盾を示す．
$\log_{10}p=\frac{n}{m}$ （m, nは整数で互いに素）…(1)
と仮定すると
$p=10^{\frac{n}{m}}$
両辺をｍ乗すると
$p^m=10^{n}$
右辺は２と５の倍数であるが，左辺のｐは素数だから，２×５の倍数ではない．矛盾
したがって， $\log_{10}p$ は無理数 →閉じる←

【例題２】
$\sqrt{2}$ が無理数であることを用いて，次のことを証明せよ．

a, bを有理数とするとき， $a+ b\sqrt{2}=0$ ならば，a=b=0になる．

（解答）

$a+ b\sqrt{2}=0$ のときにa≠0またはb≠0であれば矛盾が生じることを示す．

$a+ b\sqrt{2}=0$ のとき
　b≠0ならば $\sqrt{2}=-\frac{a}{b}$
となるが，有理数の商は有理数であるから，有理数である右辺が無理数である左辺と等しいことになり，矛盾
よって，b=0が成り立つ

$a+ b\sqrt{2}=0$ にb=0を代入するとa=0になる

以上により，a=b=0が成り立つ

【問題2.1】
以下の問いに答えよ．ただし， $\sqrt{2},\hspace{5}\sqrt{3},\hspace{5}\sqrt{6}$ が無理数であることは使ってよい．
(1)　有理数p, q, rについて， $p+ q\sqrt{2}+ r\sqrt{3}=0$ ならば，p=q=r=0であることを示せ． (1999年京都大学.前期入試問題)

参考答案を見る参考答案を隠す

（解答）
$p+ q\sqrt{2}=-r\sqrt{3}$ の各辺を2乗すると
$p^2+ 2pq\sqrt{2}+ 2q^2=3r^2$
pq≠0ならば
$\sqrt{2}=\frac{3r^2-p^2-2q^2}{2pq}$
有理数は四則演算について閉じているから，右辺は有理数．左辺は無理数であるから，矛盾
したがって，pq=0でなければならない．

(ア) p=0のとき
$q\sqrt{2}+ r\sqrt{3}=0$
の両辺に $\sqrt{2}$ を掛けると
$2q+ r\sqrt{6}=0$

r≠0ならば
$\sqrt{6}=-\frac{2q}{r}$
右辺は有理数，左辺は無理数となって，矛盾
したがって，r=0でなければならない．

このとき， $q\sqrt{2}=0$ より，q=0
以上から，p=q=r=0

(イ) p≠0のとき
pq=0からq=0だから，
$p+ r\sqrt{3}=0$
r≠0ならば
$\sqrt{3}=-\frac{p}{r}$
右辺は有理数で，左辺は無理数だから矛盾
よって，r=0でなければならない．
このとき， $p+ 0\sqrt{3}=0$ より，p=0
(イ)の分類を満たすp, q, rは存在しない．
→閉じる←

【問題2.2】
正の整数m, n (>1)について

(1) $\frac{m+ 2n}{3m+ 5n}$ が既約分数ならば， $\frac{m}{n}$ も既約分数であることを示せ．
(2) $\frac{m}{n}$ が既約分数であるならば， $\frac{m+ 2n}{3m+ 5n}$ も既約分数であることを示せ．

参考答案を見る参考答案を隠す

（解答）
(1) m, nは互いに素でないと仮定し，これらの最大公約数をg (≠1)とおくと
m=gm' , n=gn'(m', n'は正の整数)
このとき
$\frac{m+ 2n}{3m+ 5n}=\frac{gm\apos + 2gn\apos}{3gm\apos + 5gn\apos}=\frac{(m\apos + 2n\apos)g}{(3m\apos + 5n\apos)g}$
の分母分子は共通因数g (≠1)をもつことになるから，仮定に反する．
したがって，m, nは互いに素

(2) $\frac{m+ 2n}{3m+ 5n}$ が既約分数でないと仮定し，分母分子の最大公約数をg (≠1)とおくと
m+2n=ga…(i)
3m+5n=gb…(ii)(a, bは正の整数)
と書ける．
(i)(ii)の連立方程式を解くと，m=(2b−5a)g,n=(3a−b)gとなって，m, nが共通因数g (≠1)をもつことになるから，仮定に反する．
したがって， $\frac{m+ 2n}{3m+ 5n}$ は既約分数 →閉じる←

【問題2.3】
nが正の整数であるとき， $\sqrt{n^2+ 1}$ は無理数になることを示せ．

参考答案を見る参考答案を隠す

（解答）
$\sqrt{n^2+ 1}$ が有理数であると仮定すると
$\sqrt{n^2+ 1}=\frac{p}{q}$ (p, qは正の整数で，互いに素)
とおける．
両辺を２乗すると
$n^2+ 1=\frac{p^2}{q^2}$
左辺は整数だから，右辺が整数になるには
q=1…(1)
また，原式から
$\sqrt{n^2}\lt\sqrt{n^2+ 1}\lt\sqrt{(n+ 1)^2}$
$n\lt\sqrt{n^2+ 1}\lt n+ 1$
だから， $\frac{p}{q}$ は整数ではない．…(2)
(1)(2)は矛盾しているから， $\sqrt{n^2+ 1}$ が有理数であるという仮定が間違っている．
ゆえに， $\sqrt{n^2+ 1}$ は無理数 →閉じる←

【問題2.4】
nを１以上の整数とするとき，次の2つの命題はそれぞれ正しいか．正しいときは証明し，正しくないときはその理由を述べよ．

命題p：

あるnに対して， $\sqrt{n}$ と $\sqrt{n+ 1}$ は共に有理数である．

命題q：

すべてのnに対して， $\sqrt{n+ 1}-\sqrt{n}$ は無理数である．

(2007年京都大学入試問題)

参考答案を見る参考答案を隠す

（解答）
あるnに対して， $\sqrt{n}$ と $\sqrt{n+ 1}$ は共に有理数であると仮定すると，有理数の積は有理数だから
$\sqrt{n(n+ 1)}=\frac{r}{s}$ （r, sは正の整数で互いに素）
とおける．この両辺を２乗すると
$n(n+ 1)=\frac{r^2}{s^2}$
左辺は整数だから，右辺も整数になるためにはs=1…(1)
ところで
$\sqrt{n^2}\lt\sqrt{n(n+ 1)}\lt\sqrt{(n+ 1)^2}$
$n\lt\sqrt{n(n+ 1)}=\frac{r}{s}\lt n+ 1$
であるから， $\frac{r}{s}$ は整数でない…(2)
(1)(2)は矛盾であるから，命題pは正しくない．

命題qの否定：「あるnに対して， $\sqrt{n+ 1}-\sqrt{n}$ は有理数である．」と仮定すると
$\sqrt{n+ 1}-\sqrt{n}=\frac{r}{s}$ （r, sは正の整数で互いに素）
とおける．この両辺を２乗すると
$n+ 1 -2\sqrt{n(n+ 1)}+ n=\frac{r^2}{s^2}$
$\sqrt{n(n+ 1)}=n+ \frac{1}{2}-\frac{r^2}{2s^2}$
となって，右辺は有理数になるが，前半の命題pで証明したように，左辺は無理数になる．これは矛盾であるから，命題qの否定は正しくない．
したがって，命題qは正しい．

※理論上はｐ：真，ｐ：偽，ｑ：真，ｑ：偽の4通りあるはずなのに，なぜ，迷わずに上記のような答案に絞り込めるのか．
⇒ 有理数と無理数が登場する証明問題では，だいたい次のように見当を付けることができます．
　「有理数であると仮定」して，いろいろと変形していくうちに矛盾を見つけて，押出しでアウトにして，背理法により「無理数という結論」を出す．
　もし，無理数であると仮定して，いろいろと変形していくうちに矛盾を見つけようとすると，なかなか難しいのです．
　というのは，有理数は和差積商について閉じていて，有理数の中でいろいろな変形ができますが，無理数は和差積商のいずれについても閉じているとは言えません．（例えば，無理数＋無理数や無理数×無理数が無理数になるとは限りません）．このようにして，有理数が「演算についての美味しい所を皆持って行っている」ので「無理数は美味しくない残り物の集まりになっている」と見ることもできます．
　そんな訳で，有理数の中で変形して，押出しアウトの形の議論にする方が証明を進めやすいといえるので，「有理数であると仮定する」ことからスタートするのです．

→閉じる←

【問題2.5】
　nを1以上の整数とするとき，次の問いに答えよ．
(1)　 $\sqrt{n}$ が有理数ならば， $\sqrt{n}$ は整数であることを示せ．
(2)　 $\sqrt{n}$ と $\sqrt{n+ 1}$ が共に有理数であるようなnは存在しないことを示せ．
(3)　 $\sqrt{n+ 1}-\sqrt{n}$ は無理数であることを示せ．
(2016年富山大学理学部)

参考答案を見る参考答案を隠す

（解答）
(1) ***むずかしい***

　 $\sqrt{n}=\frac{q}{p}$ （p, qは正の整数で互いに素）とおくと，p=1でなければならないことを示す．
　 $p\sqrt{n}=q$ の両辺を２乗すると
　 $p^2n=q^2$
ここで，仮定によりp, qは正の整数で互いに素だから，p≠1ならば右辺がpで割り切れなくなり，矛盾を生じる.よって， p=1でなければならない．
　したがって， $\sqrt{n}$ は整数
(2)

　(1)の結果を使えば，次のように示せる．
　(1)の答案が間違っている受験生でも，(2)で(1)の結果を使った答案を書いても減点されることは「ないと思う」--別の問題だから

(1)の結果を使えば， $\sqrt{n}$ と $\sqrt{n+ 1}$ が共に有理数であるならば，共に整数になるから
$\sqrt{n}\lt\sqrt{n+ 1}\lt\sqrt{n}+ 1$
は矛盾になる．なぜなら，
１つの整数 $\sqrt{n}$ とその次の整数 $\sqrt{n}+ 1$ の間に他の整数 $\sqrt{n+ 1}$ があることになり，矛盾
(3)

　(2)の結果を使えば，次のように示せる．

(2)の結果から， $\sqrt{n}$ と $\sqrt{n+ 1}$ が共に有理数ということはない．
　そこで， $\sqrt{n+ 1}-\sqrt{n}=\frac{q}{p}$ （p, qは正の整数で互いに素）が有理数であると仮定すると
$\sqrt{n+ 1}=\sqrt{n}+\frac{q}{p}$
$\sqrt{n}=\sqrt{n+ 1}-\frac{q}{p}$
となって，
ア） $\sqrt{n}$ と $\sqrt{n+ 1}$ の一方が有理数であれば他方も有理数になる．これは「共に有理数ということはない」という(2)の結果と矛盾するから， $\sqrt{n+ 1}-\sqrt{n}=\frac{q}{p}$ が有理数であるという仮定は間違いになる．
イ） $\sqrt{n}$ と $\sqrt{n+ 1}$ の両方とも無理数である場合
$\sqrt{n+ 1}=\sqrt{n}+\frac{q}{p}$ の辺々を2乗すると
$n+ 1=n+ 2\sqrt{n}\times\frac{q}{p}+\frac{q^2}{p^2}$
$\sqrt{n}=(1-\frac{q^2}{p^2})\times\frac{p}{2q}$
となって， $\sqrt{n}$ が無理数という仮定に反する．これは矛盾であるから， $\sqrt{n}$ と $\sqrt{n+ 1}$ の両方とも無理数である場合は， $\sqrt{n+ 1}-\sqrt{n}$ は無理数になる．
→閉じる←

【例題3】
　a, b, cを自然数とする．
(3)　abc, ab+bc+ca, a+b+cがすべて偶数ならば，a, b, cはすべて偶数であることを示せ． (2016年埼玉大理・工学部［一部引用］)

（解答）
(3)
x3−(a+b+c)x2+(ab+bc+ca)x−abc=(x−a)(x−b)(x−c)であるから
x3−(a+b+c)x2+(ab+bc+ca)x−abc=0の解は，x=a, b, c
そこで，abc, ab+bc+ca, a+b+cがすべて偶数ならば，
x3=(a+b+c)x2−(ab+bc+ca)x+abcの右辺は偶数になる．
xが奇数ならばx3も奇数になるから，この式は成り立たない．
よって，xは偶数．したがって，a, b, cはすべて偶数である．

（別解）
　a, b, cのうち１つだけが奇数と仮定する．（問題文はa, b, cの対称式だからaが奇数としても一般性を失わない．以下においても同様）
　このとき，a+b+cは奇数+偶数+偶数=奇数となって，仮定に反するから，１つだけが奇数ということはない．
　次に，a, b, cのうち2つだけが奇数と仮定する．問題文はa, b, cの対称式だからa, bが奇数としても一般性を失わない．
　このとき，ab+bc+ca=ab+(a+b)cは奇数+偶数=奇数となって，仮定に反するから，2つだけが奇数ということはない．
　最後に，a, b, cの全部が奇数と仮定する．
　このとき，abcは奇数となって，仮定に反するから，3つが奇数ということはない．
　以上により，a, b, cはすべて偶数である．

【問題3.1】
　a, b, cを自然数とする．
(2)　abc, ab+bc+ca, a+b+cがすべて3の倍数ならば，a, b, cはすべて3の倍数であることを示せ． (2016年津田塾大.学芸学部［一部引用］)

参考答案を見る参考答案を隠す

（解答）
(2)
x3−(a+b+c)x2+(ab+bc+ca)x−abc=(x−a)(x−b)(x−c)であるから
x3−(a+b+c)x2+(ab+bc+ca)x−abc=0の解は，x=a, b, c
そこで，abc, ab+bc+ca, a+b+cがすべて3の倍数ならば，
x3=(a+b+c)x2−(ab+bc+ca)x+abcの右辺は3の倍数になる．
ア） x=3k+1（kは整数）ならば
　x3=(3k)3+3(3k)2+3(3k)+1=3N+1は，3の倍数でないから，この式は成り立たない．
イ） x=3k−1（kは整数）ならば
　x3=(3k)3−3(3k)2+3(3k)−1=3N−1は，3の倍数でないから，この式は成り立たない．
よって，xは3の倍数．したがって，a, b, cはすべて3の倍数である．

（別解）
ア） a, b, cのうち１つだけが3の倍数と仮定する．（問題文はa, b, cの対称式だからaが3の倍数としても一般性を失わない．以下においても同様）
　このとき，a=3k, b=3l±1, c=3m±1ならばab+bc+ca=a(b+c)+bc=3M+3N±1となって，仮定に反する.
イ） a, b, cのうち2つだけが3の倍数と仮定する．（問題文はa, b, cの対称式だからa, bが3の倍数としても一般性を失わない．）
　このとき，a=3k, b=3l, c=3m±1ならばa+b+c=3N±1となって，仮定に反する.
ウ） a, b, cのうち3つとも3の倍数でないと仮定する．
　このとき，a=3k±1, b=3l±1, c=3m±1ならばabc=3N±1となって，仮定に反する.
以上から，a, b, cはすべて3の倍数である．

→閉じる←

(携帯版)...メニューに戻る

...（PC版）メニューに戻る