�y2014�N�x�Z���^�[����.���w�U�B�z��4��i�I����j
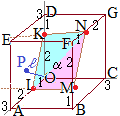
�@���W��Ԃɂ����āC������ OABC-DEFG�̒��_��
O(0, 0, 0), A(3, 0, 0), B(3, 3, 0), C(0, 3, 0)
D(0, 0, 3), E(3, 0, 3), F(3, 3, 3), G(0, 3, 3)
�Ƃ��C OD�� 2:1�ɓ�������_�� K�C OA�� 1:2�ɓ�������_�� L�Ƃ���B BF��̓_ M�C FG��̓_ N����� K, L��4�_�͓��ꕽ�ʏ�ɂ���C�l�p�` KLMN�͕��s�l�ӌ`�ł���Ƃ���B
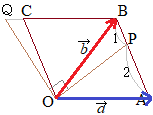
(1)�@�l�p�` KLMN�̖ʐς����߂悤�B�x�N�g��  �𐬕��ŕ\����
 =(�A�C =(�A�C�C �E�C �G)
�ƂȂ�C�l�p�` KLMN�����s�l�ӌ`�ł��邱�Ƃɂ��C  =�I =�I�ł���B �I�ɓ��Ă͂܂���̂��C����⓪�`�B�̂��������I�ׁB
�@�����ŁC M(3, 3, s), N(t, 3, 3)�ƕ\���ƁC  =�I =�I�ł���̂ŁC s=�J�C t=�L�ƂȂ�C N�� FG�� 1:�N�ɓ������邱�Ƃ��킩��B
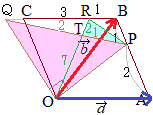
�@�܂��C  ��  �ɂ���
 �P �P�C   �R �R�@�C
  �T�V �T�V�@
�ƂȂ�̂ŁC�l�p�` KLMN�̖ʐς�  �X�Z �X�Z�@�ł���B
|
�����ǂ�
��∀�`����ɔ�]�`�l�̊��z�`∅♥
�@����������ȏ����x���̊�{���ł���C��蕶�̗U���ɏ]���ċ߂čs���C�����ł���l������D���̖��ł́C���Ԃɍ��͏o�Ȃ��Ǝv����D
(1)
K(0, 0, 2), L(1, 0, 0)������
) →�A�C,�E,�G
�l�p�` KLMN�͕��s�l�ӌ`�ł��邩��
 →�B �I
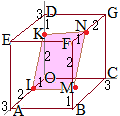 M(3, 3, s), N(t, 3, 3)
M(3, 3, s), N(t, 3, 3)�̂Ƃ��C ) ������C  �ƂȂ�ɂ�
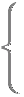 t−3=−1
3−s=2
t−3=−1
3−s=2
���C s=1, t=2→�J,�L
N(2, 3, 3)�ƂȂ邩��C GN=2, NF=1
N��FG��1:2�ɓ�������→�N
K(0, 0, 2), L(1, 0, 0), M(3, 3, 1)������C) �C �C)
 →�P →�P
 →�R →�R
 →�T�V →�T�V
�P�̉���CLK⊥LM������
��KLMN=LK×LM= →�X�Z →�X�Z
��������B����
|
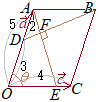 (1)
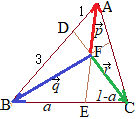
(1)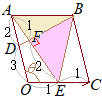 �@�E�}�ɂ����āC�O�p�`
�@�E�}�ɂ����āC�O�p�`
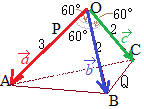 (1)
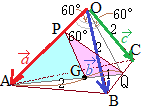
(1)
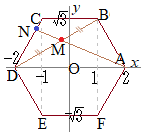 (1)
(1)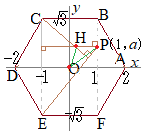 (3)
(3) (1)
(1) (1)
(1)
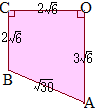 ������
������