センター試験 Ⅱ･B 統計(2013～)

→ 携帯用は別頁

=== 読者が配色を変更したい場合 ===
◎外側の色を変えるには，次の色をクリック

◎内側の色を変えるには，次の色をクリック

◎標準文字色を変えるには，次の色をクリック

== センター試験.数学Ⅱ･B.統計(2013～) ==

【2013年度センター試験.数学Ⅱ･B】第5問（選択問題）

　次の表は，あるクラスの生徒10人に対して行われた国語と英語の小テスト（各10点満点）の得点をまとめたものである。ただし，小テストの得点は整数値をとり，C>Dである。また，表の数値はすべて正確な値であり，四捨五入されていない。

番号	国語	英語
生徒1 生徒2 生徒3 生徒4 生徒5 生徒6 生徒7 生徒8 生徒9 生徒10	9 10 4 7 10 5 5 7 6 7	9 9 8 6 8 C 8 9 D 7
平均値	A	8.0
分散	B	1.00

　以下，小数の形で解答する場合，指定された桁けた数の一つ下の桁を四捨五入し，解答せよ。途中で割り切れた場合，指定された桁まで⓪にマークすること。

(1)　10人の国語の得点の平均値Aはア.イ点である。また，国語の得点の分散Bの値はウ.エオである。さらに，国語の得点の中央値はカ.キ点である。

(2)　10人の国語と英語の得点の平均値が8.0点，分散が1.00であることから，CとDの間には関係式
C+D=クケ
(C−8)2+(D−8)2=コ
が成り立つ。上の連立方程式と条件C>Dにより，C, Dの値は，それぞれサ点，シ点であることがわかる。

解説を読む

【平均値,分散,中央値】
n個のデータx1, x2, ･･･, xnの平均値 $\bar{x}$ は
$\bar{x}=\frac{x_1+ x_2+\cdots+ x_n}{n}$
分散s2は
$s^2=\frac{(x_1-\bar{x})^2+ (x_2-\bar{x})^2+\cdots+ (x_n-\bar{x})^2}{n}$
中央値は
　nが奇数個のとき，小さい順に並べて中央に来る値．n(=2m)が偶数個のとき，小さい順に並べてm番目の値とm+1番目の値の平均値とする．

(1)
(9+10+4+7+10+5+5+7+6+7)÷10=7 だから7.0→ア,イ
{(4−7)2+2(5−7)2+(6−7)2+3(7−7)2+(9−7)2+2(10−7)2}÷10=4 だから4.00→ウ,エオ
小さい順に5番目は7，6番目は7だから中央値は7.0点→カ,キ
(2)
(9+9+8+6+8+C+8+9+D+7)÷10=8 だから
　C+D=16→ク,ケ
{(6−8)2+(7−8)2+3(8−8)2+3(9−8)2+(C−8)2+(D−8)2}÷10=1 だから
　(C−8)2+(D−8)2=2→コ
この連立方程式の解は，9と7になるが､C>Dだから，C=9, D=7→サ,シ
→解説を隠す←

(3)　10人の国語と英語の得点の相関図（散布図）として適切なものはスであり，国語と英語の得点の相関係数の値はセ.ソタチである。ただし，スについては，当てはまるものを，次の⓪～③のうちから一つ選べ。

⓪

①

②

③

(4)　同じ10人に対して数学の小テスト（10点満点）を行ったところ，数学の得点の平均値はちょうど5.4点であり，分散はちょうど1.44であった。また，国語と数学の得点の相関係数はちょうど−0.125であった。
　ここで，kを1から10までの自然数として，生徒kの国語の得点をxk，数学の得点をyk，国語と数学の得点の合計xk+ykをwkで表す。このとき，国語と数学の得点の合計w1, w2, ･･･, w10の平均値はツテ.ト点である。

解説を読む

(3)
散布図は②→ス

【相関係数】
　n個の2変数データ(x1, y1), (x2, y2) ･･･, (xn, yn)の変数xに関する標準偏差をsx，変数yに関する標準偏差をsy，共分散をsxyとするとき
$s_{xy}=\frac{(x_1-\bar{x})(y_1-\bar{y})+(x_2-\bar{x})(y_2-\bar{y})+\cdots+(x_n-\bar{x})(y_n-\bar{y})}{n}$
$s_{x}=\sqrt{\frac{(x_1-\bar{x})^2+(x_2-\bar{x})^2+\cdots+(x_n-\bar{x})^2}{n}}$
$s_{y}=\sqrt{\frac{(y_1-\bar{y})^2+(y_2-\bar{y})^2+\cdots+(y_n-\bar{y})^2}{n}}$
相関係数 $r_{xy}$ は
$r_{xy}=\frac{s_{xy}}{s_xs_y}$

　国語の得点の分散は，B（ウ,エ,オ）の値から $s_{x}^2=4.00$ だから，標準偏差は $s_{x}=2.00$
　英語の得点の分散は，問題の表から1 $s_{y}^2=1.00$ だから，標準偏差は $s_{y}=1.00$
　国語と英語の得点の共分散 $s_{xy}$ は

{(9−7)(9−8)+(10−7)(9−8)+(4−7)(8−8)+(7−7)(6−8)
+(10−7)(8−8)+(5−7)(9−8)+(5−7)(8−8)+(7−7)(9−8)
+(6−7)(7−8)+(7−7)(7−8)}÷10
=(2+3+0+0+0−2+0+0+1+0)÷10=0.4

　したがって，相関係数は
$r_{xy}=\frac{s_{xy}}{s_xs_y}=\frac{0.4}{2\times 1}=0.200$ →セ,ソタチ
(4)
$\frac{(x_1+ y_1)+(x_2+ y_2)+\cdots+(x_{10}+ y_{10})}{10}$
$=\frac{x_1+ x_2+\cdots+ x_{10}}{10}+\frac{y_1+ y_2+\cdots+ y_{10}}{10}$
$=7.0+ 5.4=12.4$ →ツテ,ト
→解説を隠す←

　次に，国語と数学の得点の合計w1, w2, ･･･, w10の分散を以下の手順で求めよう。国語の得点の平均値を $\bar{x}$ ，分散を ${s_x}^2$ ，数学の得点の平均値を $\bar{y}$ ，分散を ${s_y}^2$ ，国語と数学の得点の合計の平均値を $\bar{w}$ ，分散を ${s_w}^2$ で表す。このとき
$T=(x_1-\bar{x})(y_1-\bar{y})+(x_2-\bar{x})(y_2-\bar{y})+\cdots+(x_{10}-\bar{x})(y_{10}-\bar{y})$
とおくと，国語と数学の得点の相関係数は−0.125であるから
T=ナニ.ヌネノ
である。また,kを1から10までの自然数として, $(w_{k}-\bar{w})^2$
は
$(w_{k}-\bar{w})^2=\{(x_k+ y_k)-(\bar{x}+\bar{y})\}^2$
$=\{(x_k-\bar{x})+(y_k-\bar{y})\}^2$
と変形できる。これを利用して，分散 ${s_w}^2$ は
${s_w}^2=\frac{(w_1-\bar{w})^2+(w_2-\bar{w})^2+\cdots+(w_{10}-\bar{w})^2}{10}$
$={s_x}^2+{s_y}^2+$ ハT
と表すことができるので，分散 ${s_w}^2$ の値はヒ.フヘである。ただし，ハについては，当てはまるものを，次の⓪～③のうちから一つ選べ。

⓪ $\frac{1}{2}$ 　　① $\frac{1}{5}$ 　　② $\frac{1}{10}$ 　　③ $\frac{1}{20}$

解説を読む

国語の得点の標準偏差は $s_x=2.00$
数学の得点の標準偏差は $s_w=\sqrt{1.44}=1.2$
国語の得点と数学の得点の共分散を $s_{xw}$ ，相関係数を $r_{xw}$ で表すと
$s_{xw}=\frac{T}{10}$
$r_{xw}=\frac{s_{xw}}{s_xs_w}=\frac{\frac{T}{10}}{s_xs_w}$
$-0.125=\frac{T}{10\times 2\times 1.2}$
$T=-0.125\times 10\times 2\times 1.2=-3.000$ →ナニ,ヌネノ

$(w_k-\bar{w})^2=(x_k-\bar{x})^2+(y_k-\bar{y})^2+ 2(x_k-\bar{x})(y_k-\bar{y})$
${s_w}^2=\sum_{k=1}^{10}\frac{(w_k-\bar{w})^2}{10}$
$=\sum_{k=1}^{10}\frac{(x_k-\bar{x})^2}{10}+\sum_{k=1}^{10}\frac{(y_k-\bar{y})^2}{10}+\sum_{k=1}^{10}\frac{2(x_k-\bar{x})(y_k-\bar{y})}{10}$
$={s_x}^2+{s_w}^2+\frac{1}{5}T$ →ハ
$=4.00+ 1.44+\frac{1}{5}\times(-3.000)=4.84$ →ヒ,フヘ
→解説を隠す←

【2014年度センター試験.数学Ⅱ･B】第5問（選択問題）

　次の表は，あるクラスの生徒9人に対して行われた英語と数学のテスト（各20点満点）の得点をまとめたものである。ただし，テストの得点は整数値である。また，表の数値はすべて正確な値であり，四捨五入されていないものとする。

	英語	数学
生徒1 生徒2 生徒3 生徒4 生徒5 生徒6 生徒7 生徒8 生徒9	9 20 18 18 A 18 14 15 18	15 20 14 17 8 C D 14 15
平均値	16.0	15.0
分散	B	10.00
相関係数	0.5000

(1)　生徒5の英語の得点Aはアイ点であり，9人の英語の得点の分散Bの値は，ウエ.オカである。また，9人の数学の得点の平均値が15.0点であることと，英語と数学の得点の相関係数の値が0.500であることから，生徒6の数学の得点Cと生徒7の数学の得点Dの関係式
C+D=キク
C−D=ケ
が得られる。したがって，Cはコサ点，Dはシス点である。

解説を読む

(9+20+18+18+A+18+14+15+18)÷10=16.0
A+130=144
A=14→ソタ,チ

{(9−16)2+(20−16)2+4×(18−16)2+2×(14−16)2+(15−16)2}÷9
=90÷9=10.00→ウエオカ

9人の数学の得点の平均値が15.0点であることから
(15+20+14+17+8+C+D+14+15)÷9=15.0
C+D=32→キク

英語の標準偏差をse，数学の標準偏差をsmで表すと
英語と数学の得点の相関係数の値が0.500であることから
{(9−16)(15−15)+(20−16)(20−15)+(18−16)(14−15)
+(18−16)(17−15)+(14−16)(8−15)+(18−16)(C−15)
+(14−16)(D−15)+(15−16)(14−15)+(18−16)(15−15)}
÷9÷se÷sm=0.500
20−2+4+14+2(C−15)−2(D−15)+1=45
C−D=4→ケ
したがって，C=18, D=14→コサ,シス
→解説を隠す←

(2)　9人の英語と数学の得点の相関図（散布図）として適当なものはセである。セに当てはまるものを，次の⓪～③のうちから一つ選べ。

⓪

①

②

③

解説を読む

表のデータを順に照合すると，散布図が分かる→⓪ セ
（参考）
次のボタンを押せば，「無いはずのもの」が赤で，「有るはずのもの」が緑で示される．
⇒［赤緑表示］
⇒［赤緑消去］
→解説を隠す←

(3)　生徒10が転入したので，その生徒に対して同じテストを行った。次の表は，はじめの9人の生徒に生徒10を加えた10人の得点をまとめたものである。ただし，表の数値はすべて正確な値であり，四捨五入されていないものとする。

	英語	数学
生徒1 生徒2 生徒3 生徒4 生徒5 生徒6 生徒7 生徒8 生徒9 生徒10	9 20 18 18 A 18 14 15 18 6	15 20 14 17 8 C D 14 15 F
平均値	E	14.0
分散	18.00	18.00
相関係数	0.750

　10人の英語の得点の平均値Eはソタ.チ点であり，生徒10の数学の得点Fはツ点である。

解説を読む

9人の英語の平均値は16.0だったから
$E=\frac{16.0\times 9+ 6}{10}=15.0$ →ソタ,チ
9人の数学の平均値は15.0だったから
$\frac{15.0\times 9+ F}{10}=14.0$
$F=140-135=5$ →ツ
→解説を隠す←

(4)　生徒10が転入した後で1人の生徒が転出した。残った9人の生徒について，英語の得点の平均値は10人の平均値と同じソタ.チ点，数学の得点の平均値は10人の平均値と同じ14.0点であった。転出したのは生徒テである。また，英語について，10人の得点の分散の値を $v$ ，残った9人の得点の分散を $v^{\tiny{\prime}}$ とすると

$\frac{v^{\tiny{\prime}}}{v}=$ ト
が成り立つ。さらに，10人についての英語と数学の得点の相関係数の値をr,残った9人についての英語と数学の得点の相関係数をr'とすると

$\frac{r^{\tiny{\prime}}}{r}=$ ナ
が成り立つ。ト，ナに当てはまるものを，次の⓪～⑤のうちから一つずつ選べ。ただし，同じものを選んでもよい。

⓪　−1　　①　1　　② $\frac{9}{10}$

③ $\big(\frac{9}{10}\big)^2$ 　 ④ $\frac{10}{9}$ 　　⑤ $\big(\frac{10}{9}\big)^2$

解説を読む

(4)
転出の前後で英語の平均値が変化していないから，転出者の英語の得点は15点．また，数学も平均値が変化していないから，転出者の数学の得点は14点．
以上から，転出したのは生徒8→テ

10人の英語の得点の分散は
$v=18.00$
残った9人の英語の得点の分散は
$v^{\tiny{\prime}}=\frac{18.00\times 10-(15-15)^2}{9}=20$
$\frac{v^{\tiny{\prime}}}{v}=\frac{20}{18}=\frac{10}{9}$ →④ト

10人の英語と数学の得点の相関係数は
$r=0.75$
$\frac{\frac{(.\tiny{1}.)(...)+(.\tiny{2}.)(...)+\cdot\cdot\cdot+(.\tiny{9}.)(...)+[.\tiny{10}.][...]}{10}}{\sqrt{18}\times\sqrt{18}}=0.75$
$(.\small{1}.)(...)+(.\small{2}.)(...)+\cdot\cdot\cdot+(.\small{9}.)(...)+(15-15)(14-14)=0.75\times 18\times 10=135$
10人の数学の得点の分散は18.00
残った9人の数学の得点の分散は
$\frac{18.00\times 10-(14-14)^2}{9}=20$
残った9人の英語と数学の得点の相関係数は
$r^{\tiny{\prime}}=\frac{\frac{(.\small{1}.)(...)+(.\small{2}.)(...)+\cdot\cdot\cdot+(.\small{9}.)(...)}{9}}{\sqrt{20}\times\sqrt{20}}=\frac{135}{9\times 20}=0.750$
したがって
$\frac{r^{\tiny{\prime}}}{r}=1$ →①ナ
→解説を隠す←

【2015年度センター試験.数学Ⅱ･B】第5問（選択問題）

　以下の問題を解答するにあたっては，必要に応じて29ページの正規分布表を用いてもよい。
　また，小数の形で解答する場合，指定された桁けた数の一つ下の桁を四捨五入し，解答せよ。途中で割り切れた場合，指定された桁まで⓪にマークすること。

(1)　袋の中に白球が4個，赤球が3個入っている。この袋の中から同時に3個の球を取り出すとき，白球の個数をWとする。確率変数Wについて

P(W=0)=

ア

イウ

，P(W=1)=

エオ

イウ

P(W=2)=

カキ

イウ

，P(W=3)=

ク

イウ

であり，期待値（平均）は

ケコ

サ

，分散は

シス

セソ

である。

解説を読む

(1)

【赤球,白球の確率】
　白球4個，赤球3個の合計7個が入っている袋の中から同時に3個の球を取り出すとき，白球がW個(0≦W≦3)，赤球が3−W個出る確率
• 起こりうるすべての場合の数は
$N=_7C_3=\frac{7!}{3!4!}=35$
• 白球が1個，赤球が2個出る場合の数は
$n=_4C_1\times _3C_2=12$
同様にして，W=0～3について，次の表の通りになる

白球の個数W	0	1	2	3
確率P	$\frac{_4C_0\times _3C_3}{_7C_3}$	$\frac{_4C_1\times _3C_2}{_7C_3}$	$\frac{_4C_2\times _3C_1}{_7C_3}$	$\frac{_4C_3\times _3C_0}{_7C_3}$

すなわち

白球の個数W	0	1	2	3	計
確率P	$\frac{1}{35}$	$\frac{12}{35}$	$\frac{18}{35}$	$\frac{4}{35}$	1

$P(W=0)=\frac{_4C_0\times _3C_3}{_7C_3}=\frac{1}{35}$ →ア,イ,ウ
$P(W=1)=\frac{_4C_1\times _3C_2}{_7C_3}=\frac{12}{35}$ →エ,オ,(イ,ウ)
$P(W=2)=\frac{_4C_2\times _3C_1}{_7C_3}=\frac{18}{35}$ →カ,キ,(イ,ウ)
$P(W=3)=\frac{_4C_3\times _3C_0}{_7C_3}=\frac{4}{35}$ →ク,(イ,ウ)

【期待値,分散】
　次の表で表される確率分布について

X	x1	x2	･･･	xn
P	p1	p2	･･･	pn

•期待値（平均値）E(X)は
E(X)=x1p1+x2p2+･･･+xnpn
•E(X)=mで表すとき，分散V(X)は
V(X)=(x1−m)2p1+(x1−m)2p1+･･･+(xn−m)2pn
なお，分散は次の式で求めてもよい．

X	x1	x2	･･･	xn
X2	x12	x22	･･･	xn2
P	p1	p2	･･･	pn

V(X)=E(X2)−{E(X)}2

期待値は
$E(X)=0\times\frac{1}{35}+ 1\times\frac{12}{35}+ 2\times\frac{18}{35}+ 3\times\frac{4}{35}$
$=\frac{60}{35}=\frac{12}{7}$ →ケ,コ,サ
$E(X^2)=0\times\frac{1}{35}+ 1\times\frac{12}{35}+ 4\times\frac{18}{35}+ 9\times\frac{4}{35}$
$=\frac{120}{35}=\frac{24}{7}$
も求めておくと，分散は
$V(X)=E(X^2)-\{E(X)\}^2$
$=\frac{24}{7}-\big(\frac{12}{7}\big)^2=\frac{24}{7}-\frac{144}{49}=\frac{24}{49}$ →シス,セソ
→解説を隠す←

(2)　確率変数Zが標準正規分布に従うとき
P(−タ≦Z≦タ)=0.99
が成り立つ。タに当てはまる最も適切なものを，次の⓪～③のうちから一つ選べ。

⓪ 1.64　① 1.96　② 2.33　③ 2.58

解説を読む

標準正規分布は左右対称だから，P(−z0≦Z≦z0)=2P(0≦Z≦z0)
そこで，29ページの表から0.99÷2=0.495となるz0の値を探すと，z0=2.57またはz0=2.58（ちょうど中間のz0=2.585とすれば，四捨五入してz0=2.58）→③タ
→解説を隠す←

(3) 母標準偏差σの母集団から，大きさnの無作為標本を抽出する。ただし，nは十分に大きいとする。この標本から得られる母平均mの信頼度（信頼係数）95%の信頼区間をA≦M≦Bとし，この信頼区間の幅L1をL1=B−Aで定める。
　この標本から得られる信頼度99%の信頼区間をC≦M≦Dとし，この信頼区間の幅L2をL2=D−Cで定めると
$\frac{L_2}{L_1}=$ チ.ツ
が成り立つ。また，同じ母集団から，大きさ4nの無作為標本を抽出して得られる母平均mの信頼度95%の信頼区間をE≦M≦Fとし，この信頼区間の幅L3をL3=F−Eで定める。このとき
$\frac{L_3}{L_1}=$ テ.ト
が成り立つ。

解説を読む

【母平均の推定】
　母集団からとった大きさnの標本平均が $\bar{x}$ であるとき，母平均mに対する信頼度95%の信頼区間は
$\bar{x}-1.96\times\frac{\sigma}{\sqrt{n}}\underset{=}{\lt}m\underset{=}{\lt}\bar{x}+ 1.96\times\frac{\sigma}{\sqrt{n}}$
母平均mに対する信頼度99%の信頼区間は
$\bar{x}-2.58\times\frac{\sigma}{\sqrt{n}}\underset{=}{\lt}m\underset{=}{\lt}\bar{x}+ 2.58\times\frac{\sigma}{\sqrt{n}}$

95％の信頼区間は
$\bar{x}-1.96\times\frac{\sigma}{\sqrt{n}}\underset{=}{\lt}m\underset{=}{\lt}\bar{x}+ 1.96\times\frac{\sigma}{\sqrt{n}}$
だから
$L_1=2\times 1.96\times\frac{\sigma}{\sqrt{n}}$
99%の信頼区間は
$\bar{x}-2.58\times\frac{\sigma}{\sqrt{n}}\underset{=}{\lt}m\underset{=}{\lt}\bar{x}+ 2.58\times\frac{\sigma}{\sqrt{n}}$
だから
$L_2=2\times 2.58\times\frac{\sigma}{\sqrt{n}}$
$\frac{L_2}{L_1}=\frac{2.58}{1.96}=1.31\cdot\cdot\cdot$
小数第2位を四捨五入すると，1.3→チ,ツ
$L_3=2\times 1.96\times\frac{\sigma}{\sqrt{4n}}=\frac{L_1}{2}$
$\frac{L_3}{L_1}=0.5$ →テ,ト
→解説を隠す←

正規分布表

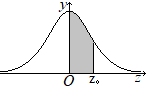　次の表は，標準正規分布の分布曲線における右図の灰色部分の面積の値をまとめたものである。

z₀	0.00	0.01	0.02	0.03	0.04	0.05	0.06	0.07	0.08	0.09
0.0	0.0000	0.0040	0.0080	0.0120	0.0160	0.0199	0.0239	0.0279	0.0319	0.0359
0.1	0.0398	0.0438	0.0478	0.0517	0.0557	0.0596	0.0636	0.0675	0.0714	0.0753
0.2	0.0793	0.0832	0.0871	0.0910	0.0948	0.0987	0.1026	0.1064	0.1103	0.1141
0.3	0.1179	0.1217	0.1255	0.1293	0.1331	0.1368	0.1406	0.1443	0.1480	0.1517
0.4	0.1554	0.1591	0.1628	0.1664	0.1700	0.1736	0.1772	0.1808	0.1844	0.1879
0.5	0.1915	0.1950	0.1985	0.2019	0.2054	0.2088	0.2123	0.2157	0.2190	0.2224
0.6	0.2257	0.2291	0.2324	0.2357	0.2389	0.2422	0.2454	0.2486	0.2517	0.2549
0.7	0.2580	0.2611	0.2642	0.2673	0.2704	0.2734	0.2764	0.2794	0.2823	0.2852
0.8	0.2881	0.2910	0.2939	0.2967	0.2995	0.3023	0.3051	0.3078	0.3106	0.3133
0.9	0.3159	0.3186	0.3212	0.3238	0.3264	0.3289	0.3315	0.3340	0.3365	0.3389
1.0	0.3413	0.3438	0.3461	0.3485	0.3508	0.3531	0.3554	0.3577	0.3599	0.3621
1.1	0.3643	0.3665	0.3686	0.3708	0.3729	0.3749	0.3770	0.3790	0.3810	0.3830
1.2	0.3849	0.3869	0.3888	0.3907	0.3925	0.3944	0.3962	0.3980	0.3997	0.4015
1.3	0.4032	0.4049	0.4066	0.4082	0.4099	0.4115	0.4131	0.4147	0.4162	0.4177
1.4	0.4192	0.4207	0.4222	0.4236	0.4251	0.4265	0.4279	0.4292	0.4306	0.4319
1.5	0.4332	0.4345	0.4357	0.4370	0.4382	0.4394	0.4406	0.4418	0.4429	0.4441
1.6	0.4452	0.4463	0.4474	0.4484	0.4495	0.4505	0.4515	0.4525	0.4535	0.4545
1.7	0.4554	0.4564	0.4573	0.4582	0.4591	0.4599	0.4608	0.4616	0.4625	0.4633
1.8	0.4641	0.4649	0.4656	0.4664	0.4671	0.4678	0.4686	0.4693	0.4699	0.4706
1.9	0.4713	0.4719	0.4726	0.4732	0.4738	0.4744	0.4750	0.4756	0.4761	0.4767
2.0	0.4772	0.4778	0.4783	0.4788	0.4793	0.4798	0.4803	0.4808	0.4812	0.4817
2.1	0.4821	0.4826	0.4830	0.4834	0.4838	0.4842	0.4846	0.4850	0.4854	0.4857
2.2	0.4861	0.4864	0.4868	0.4871	0.4875	0.4878	0.4881	0.4884	0.4887	0.4890
2.3	0.4893	0.4896	0.4898	0.4901	0.4904	0.4906	0.4909	0.4911	0.4913	0.4916
2.4	0.4918	0.4920	0.4922	0.4925	0.4927	0.4929	0.4931	0.4932	0.4934	0.4936
2.5	0.4938	0.4940	0.4941	0.4943	0.4945	0.4946	0.4948	0.4949	0.4951	0.4952
2.6	0.4953	0.4955	0.4956	0.4957	0.4959	0.4960	0.4961	0.4962	0.4963	0.4964
2.7	0.4965	0.4966	0.4967	0.4968	0.4969	0.4970	0.4971	0.4972	0.4973	0.4974
2.8	0.4974	0.4975	0.4976	0.4977	0.4977	0.4978	0.4979	0.4979	0.4980	0.4981
2.9	0.4981	0.4982	0.4982	0.4983	0.4984	0.4984	0.4985	0.4985	0.4986	0.4986
3.0	0.4987	0.4987	0.4987	0.4988	0.4988	0.4989	0.4989	0.4989	0.4990	0.4990

-29-

【2016年度センター試験.数学Ⅱ･B】第5問（選択問題）

　nを自然数とする。原点Oから出発して数直線上をn回移動する点Aを考える。点Aは，1回ごとに，確率pで正の向きに3だけ移動し，確率1−pで負の向きに1だけ移動する。ここで，0<p<1である。n回移動した後の点Aの座標をXとし，n回の移動のうち正の向きの移動の回数をYとする。
　以下の問題を解答するにあたっては，必要に応じて29ページの正規分布表を用いてもよい。

(1)　 $p=\frac{1}{3}\hspace{2}, \hspace{3}n=2$ のとき，確率変数Xのとり得る値は，小さい順に −ア，イ，ウであり，これらの値

をとる確率は，それぞれ

エ

オ

，

カ

オ

，

キ

オ

である。

解説を読む

(1)
2回のうちk (0≦k≦2)回だけ正の向きに移動する確率は $_2C_kp^k(1-p)^{2-k}$ だからXの確率分布表は

X	−2	2	6
P	$\frac{4}{9}$	$\frac{4}{9}$	$\frac{1}{9}$

→ア,イ,ウ,エ,オ,カ,キ
→解説を隠す←

(2)　n回移動したとき，XとYの間に
X=クn+ケY
の関係が成り立つ。
　確率変数Yの平均（期待値）はコ，分散はサなので，Xの平均はシ，分散はスである。コ～スに当てはまるものを，次の⓪～ⓑのうちから一つずつ選べ。ただし，同じものを繰り返し選んでもよい。

⓪ np

① np(1−p)

② $\frac{p(1-p)}{n}$

③ 2np

④ 2np(1−p)

⑤ p(1−p)

⑥ 4np

⑦ 4np(1−p)

⑧ 16np(1−p)

⑨ 4np−n

ⓐ 4np(1−p)−n

ⓑ 16np(1−p)−n

解説を読む

(2)
n回移動したとき，正の向きにY回，負の向きにn−Y回だけ移動したとすれば，点Aの座標Xは
X=(−1)(n−Y)+3Y=−n+4Y→ク,ケ
Yの平均（期待値）は
E(Y)=np→⓪コ
分散は
V(Y)=np(1−p)→①サ
Xの平均は
E(X)=E(−n+4Y)=−n+4E(Y)=−n+4np→⑨シ
分散は
V(X)=V(−n+4Y)=16V(Y)=16np(1−p)→⑧ス
→解説を隠す←

(3)　 $p=\frac{1}{4}$ のとき，1200回移動した後の点Aの座標Xが120以上になる確率の近似値を求めよう。
　(2)により，Yの平均はセソタ，標準偏差はチツであり，求める確率は次のようになる。

P(X≧120)=P $\Big($

Y−セソタ

チツ

≧テ.トナ $\Big)$

　いま，標準正規分布に従う確率変数をZとすると，n=1200 は十分に大きいので，求める確率の近似値は正規分布表から次のように求められる。
P(Z≧テ.トナ)=0.ニヌネ

解説を読む

(3)
$E(Y)=1200\times\frac{1}{4}=300$ →セソタ
$\sigma(Y)=\sqrt{1200\times\frac{1}{4}\times\frac{3}{4}}=\sqrt{225}=15$ →チツ

$X\underset{=}{\gt}120\hspace{2}\Leftrightarrow\hspace{2}-1200+ 4Y\underset{=}{\gt}120\hspace{2}\Leftrightarrow\hspace{2}Y\underset{=}{\gt}330$
$\Leftrightarrow\hspace{2}Y\underset{=}{\gt}300+ 15\times 2.00\hspace{2}\Leftrightarrow\hspace{2}\frac{Y-300}{15}\underset{=}{\gt}2.00$ →テ,トナ
正規分布表により
$P(Z\underset{=}{\gt}2.00)=0.5-0.4772=0.0228$ ≒0.023→ニヌネ
→解説を隠す←

(4)　pの値がわからないとする。2400回移動した後の点Aの座標がX=1440のとき，pに対する信頼度95%の信頼区間を求めよう。
　n回移動したときにYがとる値をyとし， $r=\frac{y}{n}$ とおくと，nが十分に大きいならば，確率変数 $R=\frac{Y}{n}$ は近似的に平均p，分散 $\frac{p(1-p)}{n}$ の正規分布に従う。
　n=2400 は十分に大きいので，このことを利用し，分散を $\frac{r(1-r)}{n}$ で置き換えることにより，求める信頼区間は
0.ノハヒ≦p≦0.フヘホ
となる。

解説を読む

【母比率の推定】
　母集団の中で，ある性質Aをもつ個体の割合をpとする．標本の大きさnが大きいとき，性質Aを持つ標本比率を $r=\frac{X}{n}$ とすると，母比率pに対する信頼度95%の信頼区間は
$r-1.96\times\sqrt{\frac{r(1-r)}{n}}\underset{=}{\lt}p\underset{=}{\lt}r+ 1.96\times\sqrt{\frac{r(1-r)}{n}}$

X=1440=−2400+4Y
Y=960
$r=\frac{960}{2400}=0.4$
$0.4-1.96\times\sqrt{\frac{0.4\times 0.6}{2400}}\underset{=}{\lt}p\underset{=}{\lt}0.4+ 1.96\times\sqrt{\frac{0.4\times 0.6}{2400}}$
$0.380\underset{=}{\lt}p\underset{=}{\lt}0.420$ →ノハヒ,フヘホ
→解説を隠す←

【2017年度センター試験.数学Ⅱ･B】第5問（選択問題）

　以下の問題を解答するにあたっては，必要に応じて29ページの正規分布表を用いてもよい。

(1)　1回の試行において，事象Aの起こる確率がp，起こらない確率が1−pであるとする。この試行をn回繰り返すとき，事象Aの起こる回数をWとする。確率変数Wの平均（期待値）mが $\frac{1216}{27}$ ，標準偏差σが $\frac{152}{27}$ であると

き，n=アイウ，p=

エ

オカ

である。

解説を読む

【二項分布の期待値，標準偏差】
　1回の試行で事象Aの起こる確率がp，起こらない確率が1−pであるとする。この試行をn回繰り返すとき，事象Aの起こる回数の期待値mは
m=np
　標準偏差σは
$\sigma=\sqrt{np(1-p)}$

(1)
$m=np=\frac{2^6\times 19}{3^3}$ ･･･(#1)
$\sigma^2=np(1-p)=\frac{2^6\times 19^2}{3^6}$ ･･･(#2)
(#2)の辺々を(#1)で割ると
$1-p=\frac{2^6\times 19^2}{3^6}\times\frac{3^3}{2^6\times 19}=\frac{19}{27}$
$p=1-\frac{19}{27}=\frac{8}{27}$ →エ,オカ･･･(#3)
さらに，(#3)を(#1)に代入すると
$n=\frac{2^6\times 19}{3^3}\times\frac{27}{8}=152$ →アイウ
→解説を隠す←

(2)　(1)の反復試行において，Wが38以上となる確率の近似値を求めよう。
　いま
$P(W\underset{=}{\gt}38)=P\Big(\frac{W-m}{\sigma}\underset{=}{\gt}-$ キ.クケ $\Big)$

と変形できる。ここで， $Z=\frac{W-m}{\sigma}$ とおき，Wの分布を正規分布で近似すると，正規分布表から確率の近似値は次のように求められる。
$P(Z\underset{=}{\gt}-$ キ.クケ)=0.コサ

解説を読む

$W\underset{=}{\gt}38\Longleftrightarrow\frac{W-m}{\sigma}\underset{=}{\gt}k\Longleftrightarrow W\underset{=}{\gt}m+ k\sigma$
とおくと
$m+ k\sigma=38$
$\frac{1216}{27}+ k\times\frac{152}{27}=38$
$\frac{2^6\times 19}{3^3}+ k\times\frac{2^3\times 19}{3^3}=2\times 19$
$2^5+ k\times 2^2=3^3$
$k=\frac{27-32}{4}=-1.25$
したがって
$W\underset{=}{\gt}38\Longleftrightarrow\frac{W-m}{\sigma}\underset{=}{\gt}-1.25$ →キ,クケ
正規分布表は左右対称だから
P(Z≧−1.25)=P(Z≦1.25)+0.5
=0.3944+0.5=0.8944≒0.89→コサ
→解説を隠す←

(3)　連続型確率変数Xのとり得る値xの範囲がs≦x≦tで，確率密度関数がf(x)のとき，Xの平均E(X)は次の式で与えられる。
$E(X)=\underset{\small{s}}{\int^{\small{t}}}xf(x)dx$
　aを正の実数とする。連続型確率変数Xのとり得る値xの範囲が−a≦x≦2aで，確率密度関数が

f(x)=

$\frac{2}{3a^2}(x+ a)$ （−a≦x≦0のとき）

$\frac{1}{3a^2}(2a-x)$ （0≦x≦2aのとき）

であるとする。このとき， $a\underset{=}{\lt}X\underset{=}{\lt}\frac{3}{2}a$ となる確率は

シ

ス

である。

また，Xの平均は

セ

ソ

である。さらに，Y=2X+7

とおくと，Yの平均は

タチ

ツ

+テである。

解説を読む

(3)
$\underset{\small{a}}{\int^{\small{\frac{3}{2}a}}}\frac{1}{3a^2}(2a-x)dx=\left[\frac{1}{3a^2}(2ax-\frac{x^2}{2})\right]_a^{\frac{3}{2}a}$
$=\frac{1}{3a^2}\{(2a\times\frac{3a}{2}-\frac{1}{2}\times\frac{9a^2}{4})-(2a^2-\frac{a^2}{2})\}$
$=\frac{1}{3a^2}(3a^2-\frac{9a^2}{8}-\frac{3a^2}{2})=\frac{1}{8}$ →シ,ス

$E(X)=\underset{\small{-a}}{\int^{\small{0}}}\frac{2}{3a^2}(x^2+ ax)dx+\underset{\tiny{0}\hspace{10}}{\int^{\small{2a}}}\frac{1}{3a^2}(2ax-x^2)dx$
$=\frac{2}{3a^2}\left[\frac{x^3}{3}+ \frac{a}{2}x^2\right]_{-a}^0+\frac{1}{3a^2}\left[ax^2-\frac{x^3}{3}\right]_0^{2a}$
$=\frac{2}{3a^2}\{0-(\frac{-a^3}{3}+ \frac{a^3}{2}\}+\frac{1}{3a^2}\{a\times 4a^2-\frac{8a^3}{3}\}$
$=-\frac{a}{9}+\frac{4a}{9}=\frac{a}{3}$ →セ,ソ

【確率変数の1次式の期待値】
a, bが定数で，Y=aX+bのとき
E(Y)=aE(X)+b

Y=2X+7のとき
$E(Y)=2\times E(X)+ 7$
$=\frac{2a}{3}+ 7$ →タチ,ツ,テ

♪∀～勝手に批評～個人の感想～∅♥
　2017年度の数学Ⅱ, B--確率分布・統計の問題は，公式に当てはめれば解けるものばかりで，内容的に難しいものではない．ただし，試験会場でこれらの分数計算を間違わずにやり切るのは大変．

→解説を隠す←

【2018年度センター試験.数学Ⅱ･B】第5問（選択問題）

　以下の問題を解答するにあたっては，必要に応じて29ページの正規分布表を用いてもよい。

(1)　aを正の整数とする。2, 4, 6, ･･･, 2aの数字がそれぞれ一つずつ書かれたa枚のカードが箱に入っている。この箱から1枚のカードを無作為に取り出すとき，そこに書かれた数字を表す確率変数をXとする。このとき，

X=2aとなる確率は

ア

イ

である。

　a=5とする。Xの平均（期待値）はウ，Xの分散はエである。また，s, tは定数でs>0のとき，sX+tの平均が20，分散が32となるようにs, tを定めると，s=オ，t=カである。このとき，sX+tが20以上である確率は0.キである。

解説を読む

(1)
X=2aとなる確率は $\frac{1}{a}$ →ア,イ

【期待値，分散】
期待値
E(X)=m=x1 p1+x2 p2+･･･+xn pn
分散
V(X)=σ2=(x1−m)2p1+(x2−m)2p2+･･･+(xn−m)2pn
　　または
V(X)=σ2=E(X2)−{E(X)}2

-表1-
X	2	4	6	8	10
P	$\frac{1}{5}$	$\frac{1}{5}$	$\frac{1}{5}$	$\frac{1}{5}$	$\frac{1}{5}$

$E(X)=m=(2+ 4+ 6+ 8+ 10)\times\frac{1}{5}=\frac{30}{5}=6$ →ウ

-表2-
X2	4	16	36	64	100
P	$\frac{1}{5}$	$\frac{1}{5}$	$\frac{1}{5}$	$\frac{1}{5}$	$\frac{1}{5}$

$E(X^2)=(4+ 16+ 36+ 64+ 100)\times\frac{1}{5}=\frac{220}{5}=44$
$V(X)=E(X^2)-\{E(X)\}^2=44-36=8$ →エ

【Y=aX+bの期待値，分散】
期待値
E(Y)=aE(X)+b
分散
V(Y)=a2V(X)

E(sX+t)=sE(X)+t=6s+t=20･･･(#1)
V(sX+t)=s2V(X)=8s2=32･･･(#2)
(#1)(#2)より
s=2, t=8→オ,カ
P(Y=2X+8≧20)=P(X≧6)

-表3-
Y	12	16	20	24	28
P	$\frac{1}{5}$	$\frac{1}{5}$	$\frac{1}{5}$	$\frac{1}{5}$	$\frac{1}{5}$

表1から
P(X≧6)=3÷5=0.6→キ
《別解》
右図3から直接計算してもよい
→解説を隠す←

(2)　(1)の箱のカードの枚数aは3以上とする。この箱から3枚のカードを同時に取り出し，それらのカードを横一列に並べる。この試行において，カードの数字が左から小さい順に並んでいる事象をAとする。このとき，事象Aの起

こる確率は

ク

ケ

である。

　この試行を180回繰り返すとき，事象Aが起こる回数を表す確率変数をYとすると，Yの平均mはコサ，Yの分散σ2はシスである。ここで，事象Aが18回以上36回以下起こる確率の近似値を次のように求めよう。

　試行回数180は大きいことから，Yは近似的に平均m=コサ，標準偏差σ= $\sqrt{\hspace{30px;}}$ シス　の正規分布に従うと考

えられる。ここで， $Z=\frac{Y-m}{\sigma}$ とおくと，求める確率の近似値は次のようになる。

$P(18\underset{=}{\lt}Y\underset{=}{\lt}36)=P(-$ セ.ソタ $\underset{=}{\lt}Z\underset{=}{\lt}$ チ.ツテ)
=0.トナ

解説を読む

(2)
ある取り出し方の１組（3枚）について
横1列に並べる並べ方の総数は，N=3!=6（通り）
その各々について，カードの数字が左から小さい順に並んでいる場合の数は､1（通り）
確率は $\frac{1}{6}$ →ク,ケ

$p=\frac{1}{6},\hspace{3}n=180$ の二項分布の平均は
$m=180\times\frac{1}{6}=30$ →コ,サ
分散は
$\sigma^2=180\times\frac{1}{6}\times\frac{5}{6}=25$ →シ,ス

18=30−5×2.4
36=30+5×1.2
P(18≦Y≦36)=P(−2.4≦Z≦1.2)=0.4918+0.3849
=0.8767≒0.88→トナ
→解説を隠す←

(3)　ある都市での世論調査において，無作為に400人の有権者を選び，ある政策に対する賛否を調べたところ，320人が賛成であった。この都市の有権者全体のうち，この政策の賛成者の母比率pに対する信頼度95%の信頼区間を求めたい。
　この調査での賛成者の比率（以下，これを標本比率という）は0.ニである。標本の大きさが400と大きいので，二項分布の正規分布による近似を用いると，pに対する信頼度95%の信頼区間は
0.ヌネ≦p≦0.ノハ
である。

　母比率pに対する信頼区間A≦p≦Bにおいて，B−Aをこの信頼区間の幅と呼ぶ。以下，Rを標本比率とし，pに対する信頼度95%の信頼区間を考える。
　上で求めた信頼区間をL1
　標本の大きさが400の場合にR=0.6が得られたときの信頼区間の幅をL2
　標本の大きさが500の場合にR=0.8が得られたときの信頼区間の幅をL3とする。このとき，L1, L2, L3についてヒが成り立つ。ヒに当てはまるものを，次の⓪～⑤のうちから一つ選べ。

⓪ L1<L2<L3　① L1<L3<L2　② L2<L1<L3
③ L2<L3<L1　④ L3<L1<L2　⑤ L3<L2<L1

解説を読む

【母平均の推定】
　母平均m，母標準偏差σの母集団から抽出された大きさnの無作為標本の標本平均をXとするとき，母平均mに対する信頼度95%の信頼区間は
$\bar{X}-1.96\times\frac{\sigma}{n}\underset{=}{\lt}m\underset{=}{\lt}\bar{X}+ 1.96\times\frac{\sigma}{n}$ ･･･(1)

母標準偏差σが未知のとき，標本標準偏差sを用いてもよい．

$r=\frac{X}{n}$ の期待値は
$\frac{1}{n}\bar{X}=\frac{1}{n}\cdot np=p$

$r=\frac{X}{n}$ の分散は
$\frac{1}{n^2}\bar{X}=\frac{1}{n^2}\cdot np(1-p)=\frac{p(1-p)}{n}$
　　標準偏差は
$\sqrt{\frac{p(1-p)}{n}}$
だから，母比率pに対する信頼度95%の信頼区間は
$r-1.96\times\sqrt{\frac{p(1-p)}{n}}\underset{=}{\lt}p\underset{=}{\lt}r+ 1.96\times\sqrt{\frac{p(1-p)}{n}}$
ここでnが十分大きいとき，大数の法則によりrはpに近いとに見なせるから，根号内のpをrに替えると(2)になる．

(3)
$r=\frac{320}{400}=0.8$ →ニ
$0.8-1.96\times\sqrt{\frac{0.8\times 0.2}{400}}=0.8-1.96\times 0.02$
$=0.8-0.039=0.761$ ≒0.76→ヌネ
$0.8+ 1.96\times\sqrt{\frac{0.8\times 0.2}{400}}=0.8+ 1.96\times 0.02$
$=0.8+ 0.039=0.839$ ≒0.84→ノハ

$L_1=2\times 1.96\times\sqrt{\frac{0.8\times 0.2}{400}}=2\times 1.96\times\sqrt{0.0004}$
$L_2=2\times 1.96\times\sqrt{\frac{0.6\times 0.4}{400}}=2\times 1.96\times\sqrt{0.0006}$
$L_3=2\times 1.96\times\sqrt{\frac{0.8\times 0.2}{500}}=2\times 1.96\times\sqrt{0.00032}$
だから
$L_3\lt L_1\lt L_2$ →④ヒ
→解説を隠す←

【2019年度センター試験.数学Ⅱ･B】第5問（選択問題）

　以下の問題を解答するにあたっては，必要に応じて29ページの正規分布表を用いてもよい。

(1)　ある食品を摂取したときに，血液中の物質Aの量がどのように変化するか調べたい。食品摂取前と摂取してから3時間後に，それぞれ一定量の血液に含まれる物質Aの量（単位はmg）を測定し，その変化量，すなわち摂取後の量から摂取前の量を引いた値を表す確率変数をXとする。Xの期待値（平均）はE(X)=−7，標準偏差はσ(X)=5とする。
　このとき，A2の期待値はE(X2)=アイである。

　また，測定単位を変更してW=1000Xとすると，その期待値はE(W)=−7×10ウ，分散はV(W)=5エ×10オとなる。

解説を読む

(1)

【期待値，分散】
期待値
E(X)=m=x1 p1+x2 p2+･･･+xn pn
分散
V(X)=σ2=(x1−m)2p1+(x2−m)2p2+･･･+(xn−m)2pn
　または
V(X)=σ2=E(X2)−{E(X)}2

V(X)=σ2=E(X2)−{E(X)}2にE(X)=−7, σ=5を代入すると
25=E(X2)−49
E(X2)=74→アイ

【Y=aX+bの期待値，分散】
期待値
E(Y)=aE(X)+b
分散
V(Y)=a2V(X)

W=1000Xの変換により
E(W)=1000E(X)=−7×103→ウ
V(W)=1000000V(X)=25000000=52×106→エ,オ
→解説を隠す←

(2)　(1)のXが正規分布に従うとするとき，物質Aの量が減少しない確率P(X≧0)を求めよう。この確率は
$P(X\underset{=}{\gt}0)=P\Big(\frac{X+ 7}{5}\underset{=}{\gt}$ カ.キ $\Big)$
であるので，標準正規分布に従う確率変数をZとすると，正規分布表から，次のように求められる。
P(Z≧カ.キ)=0.クケ･･･①
　無作為に抽出された50人がこの食品を摂取したときに，物質Aの量が減少するか，減少しないかを考え，物質Aの量が減少しない人数を表す確率変数をMとする。Mは二項分布B(50, 0.クケ)に従うので，期待値はE(M)=コ.サ，標準偏差はσ(M)= $\sqrt{\hspace{96px;}}$ シ.ス　となる。ただし，0.クケは①で求めた小数第2位までの値とする。

解説を読む

(2)

$X\underset{=}{\gt}0\Longleftrightarrow \frac{X+ 7}{5}\underset{=}{\gt}k$ とおくと
$k=\frac{7}{5}=1.4$ →カ,キ
正規分布表から
$P(Z\underset{=}{\gt}1.4)=0.5-0.4192=0.0802$ ≒0.08→ク,ケ

【二項分布の期待値，標準偏差】
　1回の試行で事象Aの起こる確率がpである試行をn回行う二項分布は，記号B(n, p)で表される．
　二項分布B(n, p)の期待値はnp，標準偏差は $\sigma=\sqrt{np(1-p)}$ に等しい．

E(M)=50×0.08=4.0→コ,サ
$\sigma(M)=\sqrt{50\times 0.08\times 0.92}=\sqrt{3.68}$ ≒ $\sqrt{3.7}$ →シ,ス
→解説を隠す←

(3)　(1)の食品摂取前と摂取してから3時間後に，それぞれ一定量の血液に含まれる別の物質Bの量（単位はmg）を測定し，その変化量，すなわち摂取後の量から摂取前の量を引いた値を表す確率変数をYとする。Yの母集団分布は母平均m，母標準偏差6をもつとする。mを推定するため，母集団から無作為に抽出された100人に対して物質Bの変化量を測定したところ，標本平均Yの値は−10.2であった。

　このとき，Yの期待値はE(Y)=m，標準偏差はσ(Y)=セ.ソである。Yの分布が正規分布で近似できると

すれば，Z=

Y−m

セ.ソ

は近似的に正規分布に従うと

みなすことができる。

　正規分布表を用いて|Z|≦1.64となる確率を求めると0.タチとなる。このことを利用して，母平均mに対する信頼度タチ%の信頼区間，すなわち，タチ%の確率でmを含む信頼区間を求めると，ツとなる。ツに当てはまる最も適当なものを，次の⓪～③のうちから一つ選べ。

⓪ −11.7≦m≦−8.7　　① −11.4≦m≦−9.0
② −11.2≦m≦−9.2　　③ −10.8≦m≦−9.6

解説を読む

(3)
　母標準偏差がσ=6，標本の大きさがn=100のとき，標本平均の標準偏差は
$\frac{\sigma}{\sqrt{n}}=\frac{6}{\sqrt{100}}=0.6$ →セ,ソ
　正規分布表から0≦Z≦1.64となる確率は，0.4495だから，P(|Z|≦1.64)=2×0.4495=0.8990≒0.90→タ,チ
−10.2+1.64×0.6=−9.216≒−9.2
−10.2−1.64×0.6=−11.184≒−11.2→②ツ
→解説を隠す←

【2020年度センター試験.数学Ⅱ･B】第5問（選択問題）

　以下の問題を解答するにあたっては，必要に応じて29ページの正規分布表を用いてもよい。

　ある市の市立図書館の利用状況について調査を行った。

(1)　ある高校の生徒720人全員を対象に，ある1週間に市立図書館で借りた本の冊数について調査を行った。
　その結果，1冊も借りなかった生徒が612人，1冊借りた生徒が54人，2冊借りた生徒が36人，3冊借りた生徒が18人であった。4冊以上借りた生徒はいなかった。
　この高校の生徒から1人を無作為に選んだとき，その生徒が借りた本の冊数を表す確率変数をXとする。

このとき，Xの平均（期待値）はE(X)=

ア

イ

であり，

X2の平均はE(X2)=

ウ

エ

である。よって，Xの標準

偏差はσ(X)=

$\sqrt{\hspace{50px;}}$ オ　

カ

である。

解説を読む

(1)

-- 度数分布表 1--
X	0	1	2	3	計N
n	612	54	36	18	720

$\Downarrow$ -- 相対度数分布表 2--
X	0	1	2	3	計
$\frac{n}{N}$	$\frac{17}{20}$	$\frac{3}{40}$	$\frac{1}{20}$	$\frac{1}{40}$	1

$\Downarrow$ -- 確率分布表 3--
X	0	1	2	3	計
P	$\frac{17}{20}$	$\frac{3}{40}$	$\frac{1}{20}$	$\frac{1}{40}$	1

$\Downarrow$ -- 確率分布表 4--
X2	0	1	4	9	計
P	$\frac{17}{20}$	$\frac{3}{40}$	$\frac{1}{20}$	$\frac{1}{40}$	1

　右の確率分布表 3から，Xの期待値を求める
$E(X)=0\times\frac{17}{20}+ 1\times\frac{3}{40}$
$+ 2\times\frac{1}{20}+ 3\times\frac{1}{40}$
$=\frac{10}{40}=\frac{1}{4}$ →ア,イ
　また，確率分布表 4からX2の期待値を求める
$E(X^2)=0\times\frac{17}{20}+ 1\times\frac{3}{40}$
$+ 4\times\frac{1}{20}+ 9\times\frac{1}{40}$
$=\frac{20}{40}=\frac{1}{2}$ →ウ,エ

【分散】
V(X)=σ2=E(X2)−{E(X)}2

上で求めた値をσ2=E(X2)−{E(X)}2
に代入すると
$\sigma^2=\frac{1}{2}-(\frac{1}{4})^2=\frac{7}{16}$
$\sigma=\frac{\sqrt{7}}{4}$ →オ,カ
→解説を隠す←

(2)　市内の高校生全員を母集団とし，ある1週間に市立図書館を利用した生徒の割合（母比率）をpとする。この母集団から600人を無作為に選んだとき，その1週間に市立図書館を利用した生徒の数を確率変数Yで表す。

　p=0.4のとき，Yの平均はE(Y)=キクケ，標準偏差

はσ(Y)=コサになる。ここで，Z=

Y−キクケ

コサ

とお

くと，標本数600は十分に大きいので，Zは近似的に標準正規分布に従う。このことを利用して，Yが215以下になる確率を求めると，その確率は0.シスになる。

また，p=0.2のとき，Yの平均はキクケの

セ

倍,

標準偏差はコサの

$\sqrt{\hspace{50px;}}$ ソ　

倍である。

解説を読む

(2)
$E(Y)=n\times p=6000\times 0.4=240$ →キクケ
$\sigma(Y)=\sqrt{np(1-p)}=\sqrt{600\times 0.4\times 0.6}=\sqrt{144}=12$ →コサ
P(Y≦215)=P(Y≦m−2.08σ)=P(Z≦−2.08)
=P(Z≧2.08)
29ページの正規分布表により
P(Z≧2.08)=0.5−0.4812=0.0188≒0.02→シス

また，p=0.2のとき，E(Y’)=600×0.2=120
これは，E(Y)=600×0.4=240の $\frac{1}{2}$ 倍→セ
$\sigma\apos=\sqrt{600\times0.2\times 0.8}$ と $\sigma=\sqrt{600\times0.4\times 0.6}$ の比を求めると
$\frac{\sigma\apos}{\sigma}=\frac{\sqrt{0.16}}{\sqrt{0.24}}=\sqrt{\frac{16}{24}}=\sqrt{\frac{2}{3}}=\frac{\sqrt{2}}{3}$ →ソ倍
→解説を隠す←

(3)　市立図書館に利用者登録のある高校生全員を母集団とする。1回当たりの利用時間（分）を表す確率変数をWとし，Wは母平均m，母標準偏差30の分布に従うとする。この母集団から大きさnの標本W1 , W2 , ···, Wnを無作為に抽出した。
　利用時間が60分をどの程度超えるかについて調査するために
U1=W1−60, U2=W2−60, ···, Un=Wn−60
とおくと，確率変数U1, U2, ···, Unの平均と標準偏差はそれぞれ
E(U1)=E(U2)= ··· =E(Un)=m−タチ
σ(U1)=σ(U2)= ··· =σ(Un)=ツテ
である。

　ここで，t=m−60として，tに対する信頼度95%の信頼区間を求めよう。この母集団から無作為抽出された100人の生徒に対してU1, U2, ···, U100の値を調べたところ，その標本平均の値が50分であった。標本数は十分大きいことを利用して，この信頼区間を求めると
トナ.ニ≦t≦ヌネ.ノ
になる。

解説を読む

(3)

【Y=aX+bの期待値，分散】
期待値
E(Y)=aE(X)+b
分散
V(Y)=a2V(X)

各々のkについて，Uk=Wk−600だから
E(Uk)=E(Wk)−600=m−600→タ,チ
σ(Uk)=σ(Wk)=30→ツ,テ

※各々のWkは母集団から抽出された大きさ1の標本の値だから母平均，母標準偏差に等しい．後に出てくる，標本平均を確率変数とした場合の $E(\bar{X})=E(X),\hspace{3}\sigma(\bar{X})=\frac{\sigma}{\sqrt{n}}$ と同じものではない．（特に標準偏差の値は等しくない）

$50-1.96\times\frac{30}{\sqrt{100}}\underset{=}{\lt}t\underset{=}{\lt}50+ 1.96\times\frac{30}{\sqrt{100}}$
$50-5.88\underset{=}{\lt}t\underset{=}{\lt}50+ 5.88$
44.12≦t≦55.88
44.1≦t≦55.9→トナ,ニ,ヌネ,ノ
→解説を隠す←

...（PC版）メニューに戻る