|
=== �ǎ҂��z�F��ύX�������ꍇ ===
���O���̐F��ς���ɂ́C���̐F���N���b�N
== �ߎ��� ==
�y�v�_1�z�@�P���̋ߎ���
�i����jh��0�̂Ƃ��Cf(a+h) �� f(a)+f’(a)h���(1) x��0�̂Ƃ��Cf(x) �� f(0)+f’(0)x���(2)
�@�����@�̉��p�Ƃ��ċߎ���(1)�������ɂ́C�u�����W�����玦���v���@�Ɓu���ϒl�̒藝���玦���v���@���l�����邪�C�ŋ߂̍��Z���w�V�̋��ȏ��ł́i�茳�ɂ���S���ɂ��āj����Ȃ��u�����W�����玦���v�����̗p����Ă���̂ŁC���̋��ނ��������饥����k���猩��C�����W���̕����悭�g���C�e���݂₷���C���t���₷���̂�������Ȃ��D
|
(1)← �@��f(x)��x=a�ɂ���������W��f’(a)�� �Œ�`�����D���������āCh��0�ɏ\���߂��l�ł���Ƃ��� �����藧�D���Ȃ킿 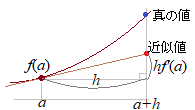 (1)�ɂ����āC����a=0�̏ꍇ���l����� �ϐ���x�ɂ���� �@�萔��h�́ix�́j�P�����܂ł��g���ĕ\���������u�P���̋ߎ����v�Ƃ���. |
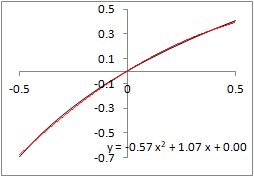
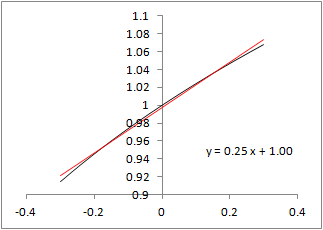 �@Excel���g���āC1���ߎ����́u���������́v�_����������@
�@Excel���g���āC1���ߎ����́u���������́v�_����������@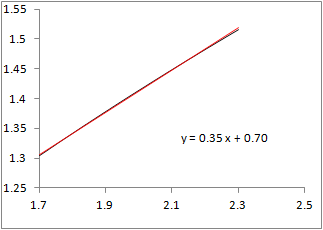
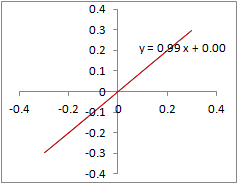
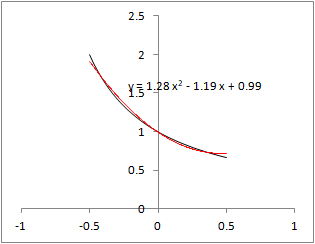
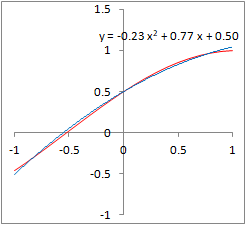
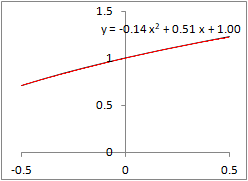 �@Excel���g���āC�Q���ߎ����́u���������́v�_����������@
�@Excel���g���āC�Q���ߎ����́u���������́v�_����������@