|
پy–â‘è8-1پzپڑپڑ
پ@‰~x2+y2=1‚ئ“_P(−2, 0)‚ً’ت‚é’¼گüy=m(x+2)‚ئ‚جŒً“_‚ًA, B‚ئ‚·‚é‚ئ‚«پCPA·PB‚جگد‚حˆê’è‚إ‚ ‚邱‚ئ‚ًژ¦‚µ‚ؤ‚‚¾‚³‚¢پD
پm‰ًگà‚ً“ا‚قپn
پi‰ً“ڑپj
ژں‚جکA—§•û’ِژ®‚ًچl‚¦‚é
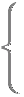 y=m(x+2)
y=m(x+2)¥¥¥(1)
x2+y2=1¥¥¥(2)
(1)‚ً(2)‚ة‘م“ü
x2+m2(x2+4x+4)=1
(m2+1)x2+4m2x+(4m2−1)=0¥¥¥(3)
(3)‚ج”»•تژ®‚ً D‚ئ‚¨‚‚ئ
D’=D/4=(2m2)2−(m2+1)(4m2−1)
=−3m2+1
ˆظ‚ب‚é‚Q“_‚إŒً‚ي‚éڈًŒڈ‚حپC D’>0‚و‚è
 \( -\dfrac{1}{\sqrt{3}}\lt m\lt\dfrac{1}{\sqrt{3}} \)¥¥¥(4) \( -\dfrac{1}{\sqrt{3}}\lt m\lt\dfrac{1}{\sqrt{3}} \)¥¥¥(4)
(4)‚جڈًŒڈ‚ج‰؛‚إ‚QŒً“_ A, B‚ج xچہ•W‚ً ƒ؟, ƒہ‚ئ‚¨‚‚ئپC(3)‚ج‰ً‚ئŒWگ”‚جٹضŒW‚©‚ç
 \( \alpha+\beta=-\dfrac{4m^2}{m^2+1} \) \( \alpha+\beta=-\dfrac{4m^2}{m^2+1} \)
 \( \alpha\beta=\dfrac{4m^2-1}{m^2+ 1} \)
A, B \( \alpha\beta=\dfrac{4m^2-1}{m^2+ 1} \)
A, B‚©‚ç xژ²‚ةچ~‚낵‚½گ‚گü‚ج‘«‚ً A', B'‚ئ‚·‚é‚ئ
 \( \rm{PA^{\tiny \prime}:AA^{\tiny\prime}:PA}=1:m:\sqrt{m^2+ 1} \) \( \rm{PA^{\tiny \prime}:AA^{\tiny\prime}:PA}=1:m:\sqrt{m^2+ 1} \)
) \( \rm{PA}=\sqrt{m^2+1}\cdot\rm{PA^{\tiny \prime}}=\sqrt{m^2+ 1}\cdot(\alpha+2) \) \( \rm{PA}=\sqrt{m^2+1}\cdot\rm{PA^{\tiny \prime}}=\sqrt{m^2+ 1}\cdot(\alpha+2) \)
 \( \rm{PB^{\tiny \prime}:BB^{\tiny\prime}:PB}=1:m:\sqrt{m^2+1} \) \( \rm{PB^{\tiny \prime}:BB^{\tiny\prime}:PB}=1:m:\sqrt{m^2+1} \)
) \( \rm{PB}=\sqrt{m^2+ 1}\cdot\rm{PB^{\tiny \prime}}=\sqrt{m^2+ 1}\cdot(\beta+ 2) \) \( \rm{PB}=\sqrt{m^2+ 1}\cdot\rm{PB^{\tiny \prime}}=\sqrt{m^2+ 1}\cdot(\beta+ 2) \)
(4)‚جڈًŒڈ‰؛‚إپC‚±‚ê‚ç‚ً—p‚¢‚é‚ئ
(\alpha%2B 2)(\beta%2B 2)) \( \rm{PA}\cdot\rm{PB}=(m^2+ 1)(\alpha+ 2)(\beta+ 2) \) \( \rm{PA}\cdot\rm{PB}=(m^2+ 1)(\alpha+ 2)(\beta+ 2) \)
\{\alpha\beta%2B 2(\alpha%2B\beta)%2B 4\}) \( =(m^2+ 1)\{\alpha\beta+ 2(\alpha+\beta)+ 4\} \) \( =(m^2+ 1)\{\alpha\beta+ 2(\alpha+\beta)+ 4\} \)
(\frac{4m^2-1}{m^2%2B 1}-\frac{8m^2}{m^2%2B 1}%2B 4)) \( =(m^2+ 1)(\dfrac{4m^2-1}{m^2+ 1}-\dfrac{8m^2}{m^2+ 1}+ 4) \) \( =(m^2+ 1)(\dfrac{4m^2-1}{m^2+ 1}-\dfrac{8m^2}{m^2+ 1}+ 4) \)
\frac{3}{m^2%2B 1}=3) \( =(m^2+ 1)\dfrac{3}{m^2+ 1}=3 \) \( =(m^2+ 1)\dfrac{3}{m^2+ 1}=3 \)
‚ئ‚ب‚ء‚ؤپCگد‚حˆê’è‚ة‚ب‚饥¥پ،ڈط–¾ڈIپ،
پ¨‰ًگà‚ً‰B‚·پ©
|
پy–â‘è8-2پzپڑپڑ
پ@a, b, r‚ًگ³‚جگ”پCm‚ًژہگ”‚ئ‚·‚éپD
پ@‰~(x−a)2+(y−b)2=r2‚ئŒ´“_O(0, 0)‚ً’ت‚é’¼گüy=mx‚ئ‚ھ‚Q“_A, B‚إŒً‚ي‚é‚ئ‚«پCOA·OB‚جگد‚ًa, b, r‚ً—p‚¢‚ؤ•\‚µ‚ؤ‚‚¾‚³‚¢پD
پm‰ًگà‚ً“ا‚قپn
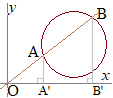
پi‰ً“ڑپj
ژں‚جکA—§•û’ِژ®‚ًچl‚¦‚é
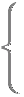 y=mx
y=mx¥¥¥(1)
(x−a)2+(y−b)2=r2¥¥¥(2)
(1)‚ً(2)‚ة‘م“ü
(x−a)2+(mx−b)2=r2
(m2+1)x2−2(a+mb)x+(a2+b2−r2)=0¥¥¥(3)
2“_‚إŒً‚ي‚é‚ئ‚«پC‚QŒً“_ A, B‚ج xچہ•W‚ً ƒ؟, ƒہ‚ئ‚¨‚‚ئپC(3)‚ج‰ً‚ئŒWگ”‚جٹضŒW‚©‚ç
 \( \alpha\beta=\dfrac{a^2+ b^2-r^2}{m^2+ 1} \)
A, B \( \alpha\beta=\dfrac{a^2+ b^2-r^2}{m^2+ 1} \)
A, B‚©‚ç xژ²‚ةچ~‚낵‚½گ‚گü‚ج‘«‚ً A', B'‚ئ‚·‚é‚ئ
 \( \rm{OA^{\tiny \prime}:AA^{\tiny\prime}:OA}=1:m:\sqrt{m^2+ 1} \) \( \rm{OA^{\tiny \prime}:AA^{\tiny\prime}:OA}=1:m:\sqrt{m^2+ 1} \)
 \( \rm{OA}=\sqrt{m^2+ 1}\cdot\rm{OA^{\tiny \prime}}=\sqrt{m^2+ 1}\cdot\alpha \) \( \rm{OA}=\sqrt{m^2+ 1}\cdot\rm{OA^{\tiny \prime}}=\sqrt{m^2+ 1}\cdot\alpha \)
 \( \rm{OB^{\tiny \prime}:BB^{\tiny\prime}:OB}=1:m:\sqrt{m^2+ 1} \) \( \rm{OB^{\tiny \prime}:BB^{\tiny\prime}:OB}=1:m:\sqrt{m^2+ 1} \)
 \( \rm{OB}=\sqrt{m^2+ 1}\cdot\rm{OB^{\tiny \prime}}=\sqrt{m^2+ 1}\cdot\beta \) \( \rm{OB}=\sqrt{m^2+ 1}\cdot\rm{OB^{\tiny \prime}}=\sqrt{m^2+ 1}\cdot\beta \)
\alpha\beta=a^2%2B b^2-r^2) \( \rm{OA}\cdot\rm{OB}=(m^2+ 1)\alpha\beta=a^2+ b^2-r^2 \) \( \rm{OA}\cdot\rm{OB}=(m^2+ 1)\alpha\beta=a^2+ b^2-r^2 \)¥¥¥پi“ڑپj
پ¨‰ًگà‚ً‰B‚·پ©
|
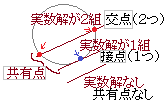 • Œً“_‚ئگع“_‚ًچ‡‚ي‚¹‚ؤ‹¤—L“_‚ئ‚¢‚¤پD
• Œً“_‚ئگع“_‚ًچ‡‚ي‚¹‚ؤ‹¤—L“_‚ئ‚¢‚¤پD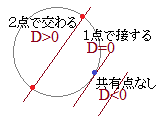
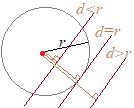
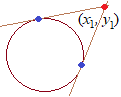 پ@ˆê”ت‚ةپC
پ@ˆê”ت‚ةپC پyگعگü‚ج’·‚³پz
پyگعگü‚ج’·‚³پz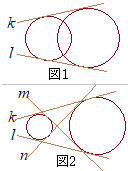 پy‹¤’تگعگü‚ج•û’ِژ®پz
پy‹¤’تگعگü‚ج•û’ِژ®پz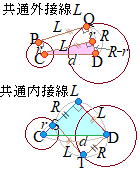 پy‹¤’تٹOگعگü‚ج’·‚³پz
پy‹¤’تٹOگعگü‚ج’·‚³پz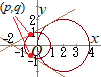 (2)‚àژg‚¤‚ئ
(2)‚àژg‚¤‚ئ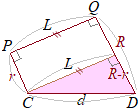 پ@‰~‚ج’†گS‚ً
پ@‰~‚ج’†گS‚ً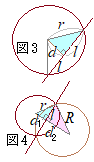 پyŒ·‚ج’·‚³پz
پyŒ·‚ج’·‚³پz پ@‰~‚ھ’¼گü‚ة‚و‚ء‚ؤگط‚èژو‚ç‚ê‚é‚à‚ج‚حپuŒتپvپC’¼گü‚ھ‰~‚ة‚و‚ء‚ؤگط‚èژو‚ç‚ê‚é‚à‚ج‚حپuŒ·پv
پ@‰~‚ھ’¼گü‚ة‚و‚ء‚ؤگط‚èژو‚ç‚ê‚é‚à‚ج‚حپuŒتپvپC’¼گü‚ھ‰~‚ة‚و‚ء‚ؤگط‚èژو‚ç‚ê‚é‚à‚ج‚حپuŒ·پv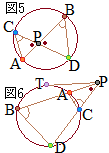 پy•û‚ׂ«‚ج’è—پz
پy•û‚ׂ«‚ج’è—پz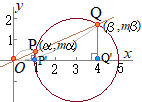 پi‰ً“ڑپj
پi‰ً“ڑپj پi‰ً“ڑپj
پi‰ً“ڑپj