|
→ スマホ用は別頁
1. 用語の整理
(1) 三平方の定理(ピタゴラスの定理),ピタゴラス数
三平方の定理は,中学校3年の数学で習う定理で,直角三角形の直角を挟む2辺の長さをa, b,斜辺の長さをcとするとき,
三平方の定理が成り立つ三角形の辺の長さには のように「三辺とも正の整数」であるものや のように「少なくとも1つの辺の長さが整数でない」ものもある. ①のように三辺とも正の整数であるとき,これら3つの数の組をピタゴラス数という.ピタゴラス数は ・・・ のように限りなくある. |
(2) フェルマー予想(フェルマーの最終定理)
フェルマー予想とは,nが3以上の整数であるとき
を満たす正の整数a, b, cは存在しないという予想のことをいう.この予想が正しいことは,1995年アンドリュー・ワイルスによって証明された.フェルマーの最終定理,フェルマーの大定理とも呼ばれる. (3) オイラー予想
オイラーは,フェルマー予想をk>3の場合に拡張して,m<kのとき
なお,これらの反例を見つけた数学者たちが,問題をさらに絞り込んで,m<k−1のとき解が存在しないとしたものを,ランダー・パーキン・セルフリッジ予想という.を満たす正の整数 20世紀になってから,この予想に対する反例が見つかった. |
|
(4) ウェアリング問題
ウェアリングは,1770年に
「すべての整数は4個以下の平方数の和として表せる」 「すべての整数は9個以下の立方数の和として表せる」 「すべての整数は19個以下の4乗数の和として表せる」 ・・・ 「すべての整数は
k=4の場合,すなわち「すべての自然数は4つの平方数の和であらわすことができる」は,ラグランジュの4平方の定理と呼ばれる.
※このウェアリング問題では,与えられた乗数kに対して,フェルマー予想やオイラー予想で考える左辺の項の個数mが遥かに多いことに注意.すなわち• のように左辺の項数を増やしていくと,解が見つかることがある. • のように左辺の項数を増やしていくと,解が見つかりやすい. このことを参考にすると,ディオファントス問題が全く解けないときは,左辺の変数の個数を増やすと少しやさしい問題に変わる傾向があるということが分かる. |
(5) ディオファントス問題(k, m, n)
与えられた正の整数k, m, nに対して
を満たす整数解を求める問題をディオファントス問題(k, m, n)という. ピタゴラス数,フェルマー予想,オイラー予想との関わりで,このページではn=1の場合,すなわち右辺が1つの数のk乗となっているもの のみ扱う. ピタゴラス数を求めることはディオファントス問題(2, 2, 1)であり,フェルマー予想はディオファントス問題(k, 2, 1) k=3, 4, 5, ・・・に対応し,オイラー予想はディオファントス問題(k, m, 1), k>m に対応するが,以下のページでは,ピタゴラス数,フェルマー予想,オイラー予想は有名なのでそのまま使い,他の組合せはディオファントス問題(k, m, 1)と呼ぶことにする. |
|
2. 問題の一覧表
|
※この表で,→2桁などと書いてあるのは,最小の整数解(例えば《5.5》で言えば,右辺の プログラミングの演習で,受講者が100人いる場合とか,賛同者をネットで募集できた場合に,区間を分けて点検すれば(協業による分業),限界は越えられるかもしれない. このサイトにあるPythonプログラムはかなり速い(Python2 のコードなのでPython3で使うには,printを( )でくくる.他,time関連の警告は無視できる) 3. パソコンと数学の役割分担
(1) 高校生が使っているパソコンでは,整数問題を総当たり的に調べていくことができるので,1つあるいは幾つかの解を見つけることは,パソコンが得意なことです. ただし,あまりに多くの数を調べるには時間がかかり過ぎるような場合とか,そのパソコンに装備されているソフトで扱える桁数の限界を超えてしまうような巨大数は調べられません. (2) 幾つかの形の問題については,数学の書物やweb記事に結果が示されていることがありますので,これらも参考にしながら調べるのがよいでしょう. (3) パソコンでは無限に多くの数を調べることはできないので,「解がない」ことを証明したり,「解が無限にある」ことを証明するには,数学を使います. |
|
4. 個別の解
《2.2》 ピタゴラス数
を満たす整数解
【要約】
(1) パソコンで総当たり的に調べて,解があれば幾つか表示する.(1) を満たす整数解 (2) この解は,互いに素な正の整数m, nを用いて と書ける.
=総当たりでピタゴラス数を求める(Pytho3のコード)=
とりあえず右辺の整数を50までとする 【例1】 IDLE → New File → Save as .. → Run
import math #1
import datetime as dt #2
dt1 = dt.datetime
nt1 = dt1.now() #3
L1 = [(3,4,5)]
def is_pythagoras(x):
global L1
for a in range(1,x):
for b in range(a, x):
for c in range(b,x):
if a**2+b**2 == c**2:
if math.gcd(math.gcd(a,b),c) == 1: #4
check1 = 0
for n in range(0, len(L1)):
if L1[n] == (a,b,c): #5
check1 = 1
break
else:
continue
if check1 == 0:
L1.append((a,b,c)) #6
for n in range(1, 51):#7
is_pythagoras(n)
print(L1,len(L1))
nt2 = dt1.now() #8
print(nt2-nt1) #9
→[(3, 4, 5), (5, 12, 13), (8, 15, 17), (7, 24, 25), (20, 21, 29), (12, 35, 37), (9, 40, 41)] 7 0:00:00.514971 #1→ 最大公約数の判定関数gcd()を使うために,mathモジュールをインポートする #2→ 所要時間を調べるために,datetimeモジュールをインポートする #3→ 初めの時刻を変数nt1に代入しておく #4→ 互いに素な組合せだけを選ぶ #5→ 同じものがあれば追加しない #6→ 同じものがなければ,追加する |
など,50以下の整数a, b, cに対して7組の解がある.c≦250まで調べると,次の表のようになる.
|
|
(3) m>n≧1を整数とするとき,次の恒等式が成り立つ. 上記の解の例[1]は,m=2, n=1から得られ,[2]は,m=3, n=2から得られ,[3]は,m=5, n=3(から公約数2で割ったもの)から得られる. このようにして,m>n≧1の整数を限りなく代入していくと,限りなく多くのピタゴラス数が得られるから,ピラゴラス数は無限にあると言える. 表(A)は,c≦250の範囲で,a, b, cが互いに素なすべてのピタゴラス数の組の一覧で,その組に対応するm, nの値が右にある. なお,このようなピタゴラス数の媒介変数表示が2変数m, n(自由度2)でなければ表現できないということではない. 両辺をn4で割ると,正の有理数 と1つの媒介変数だけで表せる. 表(B)は,表(A)に登場するc≦250の範囲のピタゴラス数をtの小さい順に並べたもの.ただし,m>n>0だから,1<tの値のみ登場する. 以上のように,m>n≧1の整数を限りなく代入していくと,限りなく多くのピタゴラス数が得られる.もしくは,1<tの有理数を限りなく代入していくと,いくらでもピタゴラス数が得られるから,次のことが言える.
【要約1】
逆に,任意のピタゴラス数,すなわちディオファントス問題(2, 2, 1)の解,互いに素である正の整数a, b, c (1≦a≦b<c)がピタゴラス数,すなわちディオファントス問題(2, 2, 1)の解は,無限に多く存在する. の形に表せることは次のように証明できる. まず,互いに素である正の整数a, b, c (1≦a≦b<c)が なぜなら, (ⅰ)「a, bとも偶数」ならば,左辺は偶数となり,これに等しいcは偶数でなければならないから,この組合せは,互いに素という仮定に反する. (ⅱ)「a, bとも奇数」ならば, となるときcは偶数になる. そこで,c=2kとおくと, (1)(2)は矛盾であり,「a, bとも奇数」という仮定は成り立たない.(cが偶数ならば,(2)に示されるように (ⅰ)(ⅱ)により,a, bは奇数と偶数,cは奇数ということが言える. そこで,a, cは奇数,bは偶数とすると ここで,c−a, c+aは,奇数−奇数,奇数+奇数だから,いずれも2で割り切れる. |
さらに,2が最大公約数で,2よりも大きい公約数pはないことは,次のように示せる. ア) c−a, c+aが,いずれも4で割り切れるとき c+a=4k’
c−a=4k”
2c=4(k’+k”)
c=2(k’+k”)
これは,cが奇数という仮定に反する.(aについても言える)よって,c−a, c+aは,いずれも2で割り切れるが,4では割り切れない. イ) c−a, c+aが,いずれも奇数の素数pで割り切れるとき c+a=pk’
c−a=pk”
2c=p(k’+k”)
2a=p(k’−k”)
pは奇数だから,a, cがpで割り切れる.a=ps c=pt(s, tは整数) とおくと となるから,bもpで割り切れることになり,a, b, cが互いに素という仮定に反する. よって,c−a, c+aは,いずれも奇数の素数を公約数として持たない. ア)イ)より, c+a=2k’
c−a=2k”
(k’, k”は奇数で互いに素)とおける.このとき により,b=2mn(m, nは互いに素)とおくと k’, k”は奇数で互いに素だから, とおける 結局 より これにより となる
【要約2】
ピタゴラス数,すなわちディオファントス問題(2, 2, 1)の解,互いに素である正の整数a, b, c (1≦a≦b<c)(a, cは奇数,bは偶数)が を満たすならば とおける |
|
《2.3~2.5》ディオファントス問題
を満たす整数解を求める. という自明解が含まれるが,for f in range(e+1, x)とすればその自明解は防げる.それ以外の プログラムとしては,前述の例1を変数6個まで増やし,for a in range(0, x)とすればよい. 所要時間約6秒で,20以下の整数211組の解が得られる. など その中には,(0が1個の)ディオファントス問題(2, 4, 1)の解が53個含まれる. など また,(0が2個の)ディオファントス問題(2, 3, 1)の解が14個含まれる. など さらに,(0が3個の)ピタゴラス数の解が3組含まれる. |
【要約】
(解説)(1) ディオファントス問題(2, 3, 1) を満たす正の整数 (2) この解は,次の媒介変数表示で表される. (2)を示せば,解が無限にあること(1)も言えるから,(2)を示す. 初めに,(2)の左向き矢印[←]については,恒等式として気長に変形していけば示せる. (左辺) = |
d<40となる組について,a, b, c, dを媒介変数m, n, p, qを使って表す具体例は次の通り.
|
[→]の証明について: の形に書けることを示せば,証明が完成するが,これはかなり難しい.(以下の原稿でも完成していない.) d<40となる組については,すべて の形に書けることは,上記の表から分かる. (証明) ア) この場合, イ) ウ) エ) |
|
*** ディオファントス問題(2,4,1)の解 ***
【要約】
d<20の範囲にある解は次の表の通り.(1) (2) 上記の解について,
ア)
イ)
ア)イ)より,
ただし,その事情は「 のような解も含まれるようになる.
|
上記要約の(2)の証明は,次の通り. (この証明は,高校生が剰余系の練習を行う場合に,難し過ぎず,やさし過ぎない,ちょうどよいレベルの問題になる) ⅰ)
左辺の和は偶数になり,右辺
ⅱ)この場合, 他方で,右辺は 他方で,右辺は 他方で,右辺は 連続する2整数の積は,2の倍数になるから, 他方で,右辺は となるから, この場合, |
|
*** ディオファントス問題(2,5,1)の解 ***
【要約】
f<20の範囲にある解は次の表の通り.(1) (2) 上記の解について,
ア)
イ)
ア)イ)より,
ただし,その事情は「 のような
|
上記要約の(2)の一部証明は,次の通り. (この証明は,高校生が剰余系の練習を行う場合に,難し過ぎず,やさし過ぎない,ちょうどよいレベルの問題になる) ⅰ) ここで連続2整数の積は2の倍数になるから,左辺は 他方,右辺は 以上により,ここからは解は出ない. 他方,右辺は 他方,右辺は 以上により,ここからは解は出ない 他方,右辺は 以上により,ここからは解は出ない 他方,右辺は
左辺は偶数になり,これに等しくなるためには右辺の
以上により,ⅱ) ⅴ) |
|
《3.2~6.2》フェルマー予想
を満たす整数解はない.
この問題は,1670年に公表されてから,1995年まで325年間も解けなかったということから分かるように,高校生が解けるような問題ではない.ただし という形で,乗数を3に限定し,cを素数に限定すれば,高校生でも解ける問題になる.以下は,1999年早稲田大学の入試問題で,答案は筆者が作成したものです.
(i) a+b≧a2−ab+b2を満たす正の整数の組(a, b)をすべて求めよ.
(ii) a3+b3=p3を満たす素数pと正の整数a, bは存在しないことを示せ.
(i) 2変数a, bの2次関数の取り得る値の範囲を求める基本は,まずbを固定してaの関数として頂点を求め,次にその各々についてbを動かして範囲を調べる. 左辺の各項は2乗で0以上だから |
b=1, 2
ア) b=1のとき(1)に代入すると a2−2a≦0 a(a−2)≦0 0≦a≦2 aは正の整数だからa=1, 2 イ) b=2のとき(1)に代入すると a2−3a+2≦0 (a−1)(a−2)≦0 1≦a≦2 aは正の整数だからa=1, 2 以上より,(a, b)=(1,1), (1,2), (2,1), (2,2) (ii) a+b≧a2−ab+b2のとき(i)の結果から a3+b3=2, 9, 9, 16となっていずれも素数の3乗にはならない. a+b<a2−ab+b2のとき (a+b)(a2−ab+b2)=p3 のとき,右辺は素数の3乗だからこれを満たすa+b, a2−ab+b2の組合せは次の表のとおり
(2) a2−ab+b2=p2…(*2) (*1)よりb=p−aを(*2)に代入すると a2−a(p−a)+(p−a)2=p2 3a2−3ap=0 3a(a−p)=0 aは正の整数だから a=p このとき b=0となって仮定に反する. 以上から,a3+b3=p3を満たす素数pと正の整数a, bが存在すると仮定すれば矛盾を生ずるから,背理法により示された. |
|
《3.3~3.5》ディオファントス問題
を満たす整数解
【要約1】
(1) ディオファントス問題(3, 2, 1)は,3次の場合のフェルマー予想にあたり,次の方程式[0]を満たす正の整数解はない. (2) ディオファントス問題(3, 3, 1),すなわち次の方程式[1]を満たす正の整数 この解のうち幾つかは,ラナヌジャンの等式などによって無限に生成できる. 次の表はd≦500の範囲で方程式[1]を満たす正の整数解の組の一覧で,YはJ.Youngの等式,Rはラマヌジャンの等式,R’はラマヌジャンの等式を参考にして筆者が作った等式,V,V’はF.Vietaの等式,JはJ.Jandasekの等式,AはG.Amponの等式としてweb記事に紹介されているもので,表中1のマークがあるところは,その等式で表現できることを表す. また,a,b,cのうち奇数が1個の組のうちで,d=25からd=499までの・・・には,これらの等式で書けない130個の解がある.同様に,a,b,cのうち奇数が2個の組のうちで,d=44からd=500までの・・・には,これらの等式で書けない137個の解があり,a,b,cのうち奇数が2個の組のうちで,d=97からd=479までの・・・には,これらの等式で書けない19個の解がある. ピタゴラス数では,すべての解に対応する媒介変数表示が存在したが,方程式[1]の正の整数解にはそのようなものは知られておらず,媒介変数表示を用いて表せるのは,解のほんの一部に過ぎない. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
(解説) (1) Wikipediaなどに,ラマヌジャンの等式として,次の式が紹介されている. |
(2) ラマヌジャンの恒等式(R)は,「a, b, cのうち2個が奇数,1個が偶数の場合だけを表す」ことを証明してみよう. とおく. x, yとも偶数のときは,a, b, c, dとも偶数になり,互いに素という条件を満たさないから,x, yの少なくとも1つは奇数でなければならない. xが偶数で,yが奇数のとき,a, cは奇数,bは偶数になる.xが奇数で,yが偶数のときも同様になる. xもyも奇数のとき,a, cは奇数,bは偶数になる. 以上により,ラマヌジャンの恒等式(R)を満たす互いに素な解a, b, cは「2個が奇数,1個が偶数」である.・・・(*2)も同様に示せる. このようにして,前述の表において,R, R’に1のマークがついている解は,奇数が2個の場合に限られることが分かる. (3) F.Vietaの等式(V)(V’)は,変数x, yが正負の整数をとり得るときは同じものになることを示してみよう. (V)式のyに−yを代入すると 移項すると となって(V’)になる. ただし,これはx, yが正負の整数をとり得る場合の話で,x, y, a, b, c, dが正の整数という条件がある場合には,(V)と(V’)は必ずしも同じではない.実際,前述の表において,V, V’で1のマークが付く解が異なっている. |
|
(4) 大まかな傾向で言えば,ディオファントス方程式(3, 3 ,1), (3, 4, 1), (3, 5, 1)すなわち次の[1][2][3]について,個数が多いほど,数字が大きいほど解は多くなる. を満たす整数解 次の表は,1つの右辺の値に対して,[1][2][3]で各々何通りの解があるのかを数えたものです.
例えば,右辺の値6,「1」の解が1通りとは のように右辺が6となる解が[1]の型で1通りだけあることを示しています. 例えば,右辺の値28,「1」の解が1通り,[2]の解が3通り,[3]の解が4通りとは,次の解を集計したものです. 表から分かるように,ディオファントス方程式(3, 5, 1)すなわち上記の[3]の形の方程式は,右辺の値が9以上のすべての整数に対して解がある. |
(5) 例えば[1]の形の方程式について 3乗,5乗,...のような奇数乗の場合には,負の数も許容すれば表せる範囲が広がる. のような物も含めて考えることもできるが,負の数や0をを許容してしまうと のような自明解が入って来るので,ここでは(*1)(*2)のようなもの以外で考えると,d≦40の範囲で次のような組がある. このように負の数を許容すると,表せる整数の範囲が広がり,右辺の値dにどんな自然数を入れても対応する左辺の値が決まる. 運悪く,d=13となる組はしぶとく登場しないが,左辺に100以上の数を使うとようやく登場する.
|
|
[1]の形で負の整数も許容した場合,一般に次のことが言える. が成り立つとき も成り立つ.(∵負の項を右辺に移項すれば分かる.) (6) J.Youngの等式とは,次の形の恒等式をいう. d≦500の範囲で,係数の大きい方では ※等式は限りなく作れるが,これらはいずれも「a, b, cのうち2個が奇数,1個が偶数の場合」だけを表す.「a, b, cのうち1個もしくは3個が奇数の場合」を表す媒介変数表示を筆者はまだ作れていない. |
【要約2】
ディオファントス問題(3, 3, 1),すなわち次の方程式[1]を満たす正の整数 ⅰ) J.Jandasekの等式,G.Amponの等式は,nが大きくなると急速に大きくなり,方程式[1]の解のうちで表現できない組が多い. いずれも,左辺のa,b,cのうち2個が偶数,1個が奇数,右辺のdは奇数になる. ⅱ)F.Vietaの等式も次数の大きな多項式になっていて,媒介変数を大きくしていくと,急速に大きくなり,方程式[1]の解のうちで表現できない組が多い. ⅲ)J.Youngの等式,ラマヌジャンの等式は,比較的多くの解をカバーできる.ただし,この等式は左辺のa,b,cのうち2個が奇数の組だけしか表せない. ⅳ)上記のどの等式によっても,左辺のa,b,cのうち3個が奇数で右辺のdも奇数の組を表すことはできない. ※)プログラミングを少し学習すると,筆者が作った等式と同レベルのものを作ることはできるかもしれない.ただし,1日の宿題のレベルでなく,1週間とか夏休みの課題のレベルになる.(筆者のやりかたは,Python3のsympyにある因数分解関数factor()を用いて,左辺の係数を網羅的に書き換えながら右辺が3乗になるものを探した.ただし,恒等式となるためには,x=1, y=0のときも等しいことが必要条件になるから,例えば1つの解(3,4,5,6)を用いて そのときに,Youngの等式のように |
※「ラマヌジャンの恒等式」補足説明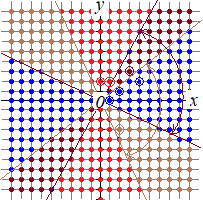 ==図1== とおくと すなわち が しかし,任意の ア) 図において,●で示した点(x, y)は,対応するa, b, cが3個とも正の整数になる組を表す. 例えば,二重丸で示した点(1, 0)には, すなわち という形で,a, b, c, dが互いに素である解の定数倍になっている.一般に,ある点(x, y)がディオファントス問題(3, 3, 1)の正の整数解 例えば,二重丸で示した(2, 1)と(4, 2)は,各々 に対応しているが,②は①の定数倍の組となっている. x=0のときは, a, b, c, d>0の条件は, (2)(4)は各々 (1)→ (3)→ 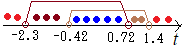 ==図2== |
イ) 図1において,●で示した点(x, y)は,対応するcが負の整数になる組を表す. 例えば,二重丸で示した点(4, 4)には, ウ) 図1において,●で示した点(x, y)は,対応するaが負の整数になる組を表す. 例えば,二重丸で示した点(2, −3)には, エ) 図1において,●で示した点(x, y)は,対応するa, cが負の整数になる組を表す. 例えば,二重丸で示した点(1, 2)には, イ)ウ)の例は各々, エ)の例は,移項すれば (1) ラマヌジャンの恒等式が1つ与えられたとき,媒介変数を1次変換して得られる恒等式もディオファントス問題(3, 3, 1)の整数解となる. 例えば に対して,媒介変数の変換 を行うと についても, |
|
※以下,個人のパソコンで総当たりで見つけることは難しいが,1つの解を示されたら,両辺が等しいことを確かめることはできるものを,茶色で示す. 《4.3》オイラー予想
を満たす整数解を求める. (知られている最小解, 1988, N.J.エルキース)
(1988, N.J.エルキース)
1958年発行の「数論における未解決問題」(リチャード・ガイ著/一松信訳/Spring-Verlag Tokyo)によれば,「現在まで
|
《4.4》ディオファントス問題
を満たす整数解を求める. など多数見つかっている (1911, R. Norrie)
《4.5》ディオファントス問題
を満たす整数解を求める. |
|
《5.3》オイラー予想
を満たす整数解を求める.
###《5.3》オイラー予想については,かなり大きな数字まで調べられているが,解は見つかっていない###
《5.4》オイラー予想
を満たす整数解を求める. (1968, L.J.ランダー, T.R.パーキン)
(2004, Frye)Wikipedia参照
《5.5》ディオファントス問題
を満たす整数解を求める. (1934, Sastry)Wikipedia参照
(1967, 最小解, Lander, Parkin, Selfridge)Wikipedia参照
今日のパソコンでは(2021年現在Window10, 32bit機, Intel i5)所要時間十数分で,f≦500の解が得られる.上記以外には |
《5.6》ディオファントス問題
を満たす整数解を求める. など 100以下の整数まで探すと,(0が1個の)ディオファントス問題(5, 5, 1)の解が2個含まれる. さらに,150以下の整数まで探すと,(0が2個の)ディオファントス問題(5, 4, 1)の解が1個含まれる. |
|
《6.3》オイラー予想
を満たす整数解を求める. 《6.3》オイラー予想すなわち,ディオファントス問題(6, 3, 1)について書かれた記事は見当たらない.解の有無について手がかりもない.
《6.4》オイラー予想
を満たす整数解を求める. 《6.5》オイラー予想すなわち,ディオファントス問題(6, 4, 1)について書かれた記事は見当たらない.解の有無について手がかりもない.
《6.5》オイラー予想
を満たす整数解を求める. 《6.5》オイラー予想すなわち,ディオファントス問題(6, 5, 1)について書かれた記事は見当たらない.解の有無について手がかりもない.
|
(参考) ディオファントス問題(6, 8, 1)の解は,多数見つかっている. など ディオファントス問題(6, 7, 1)の解は,1つ見つかっている. ディオファントス問題(6, 6, 1)について書かれた記事は見当たらない.解の有無について手がかりもない.
|