�@��{�Ə����ĂȂ��y�����z�́C�o���Ȃ��Ă��悢�̂��C�o���Ȃ���Ȃ�Ȃ��̂��C�~�~�N�O�ɕM�҂����Z������������ɂ́C���w�̐搶�ɂ����q�˂��D
�@�M�҂̍��̍l���������u�o���Ȃ��Ă��悢���v�u�K�v�ɂȂ���悢�v�D��w�����Ŏ��X�u6����1�����v�̈������b��ɂȂ�D
(x-\beta)dx=-\frac{a}{6}(\beta-\alpha)^3\]&chco=990000)
�@���̖����o���ƁC�o���ė����҂͂����ɂł��C�o���ė��Ȃ������҂͎��Ԃ�������̂ŁC���̖��Ɋ����鎞�Ԕz�����ς��C���͂�v�l�͂ƈقȂ链�_���z�ɂȂ��Ă��܂��Ƃ����b�D���̑g�ݍ��킹���l�����ɏo�肷���w�́C���ҊO��̊w�������Ă��܂����ƂɂȂ�D
�@�������o���ė��������Ŏ�悤�Ȑ��w�̎����́C���܂芴�S���Ȃ����C�t�Ɋ�����āC�ȒP�Ȍ������o���Ă����獇�i�����āC�w�������m�ۂ��邱�Ƃ����肩�ȁD�P���̂��ƂłȂ��C���v�Ƌ����̃o�����X�Ő��藧���E�������Ă���D
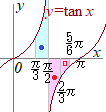
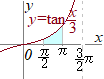
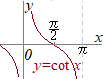
 taylor�����Ō�����
taylor�����Ō�����